题目内容
(本题满分12分)
已知函数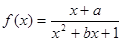 是奇函数,
是奇函数,
①求实数a和b的值;
②判断函数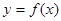 在
在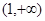 的单调性,并利用定义加以证明
的单调性,并利用定义加以证明
已知函数
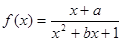 是奇函数,
是奇函数,①求实数a和b的值;
②判断函数
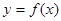 在
在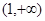 的单调性,并利用定义加以证明
的单调性,并利用定义加以证明解:(1) …………………………………2分
…………………………………2分
又因 ,即
,即 ,
,
 ………………………………………………………………..4分
………………………………………………………………..4分
(2)函数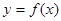 在
在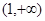 单调递减……………………………………….6分
单调递减……………………………………….6分
证明:任取 ,设
,设 ,
,
则


 ;
;
 ,
,
 ,
,
函数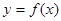 在
在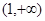 单调递减……………………………………12分
单调递减……………………………………12分
 …………………………………2分
…………………………………2分又因
 ,即
,即 ,
, ………………………………………………………………..4分
………………………………………………………………..4分(2)函数
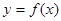 在
在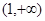 单调递减……………………………………….6分
单调递减……………………………………….6分证明:任取
 ,设
,设 ,
,则



 ;
;
 ,
,
 ,
,
函数
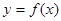 在
在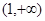 单调递减……………………………………12分
单调递减……………………………………12分本题考查函数的奇偶性和单调性。第(1)小题是考查函数的奇偶性,需要运用奇函数的定义及性质求出参数 ,
, 的值;第(2)小题是考查函数的单调性,需要运用递减函数的定义,解题的步骤:任取,作差,变形,判号,下结论。
的值;第(2)小题是考查函数的单调性,需要运用递减函数的定义,解题的步骤:任取,作差,变形,判号,下结论。
 ,
, 的值;第(2)小题是考查函数的单调性,需要运用递减函数的定义,解题的步骤:任取,作差,变形,判号,下结论。
的值;第(2)小题是考查函数的单调性,需要运用递减函数的定义,解题的步骤:任取,作差,变形,判号,下结论。
练习册系列答案
相关题目
 在
在 上为增函数,且f(
上为增函数,且f( )=
)= ,f(1)=2,集合
,f(1)=2,集合 ,关于
,关于 的不等式
的不等式 的解集为
的解集为 ,求使
,求使 的实数
的实数 的取值范围.
的取值范围.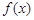 是定义在R上的函数,且对任意
是定义在R上的函数,且对任意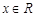 ,满足
,满足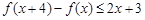 ,
,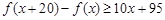 ,且
,且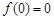 ,则
,则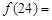 ______
______ 的单调递减区间是 ( )
的单调递减区间是 ( ) 若存在
若存在 ,当
,当 时,
时, ,则
,则 的取值范围是 ▲
的取值范围是 ▲ 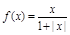 (x
(x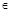 R),四位同学甲、乙、丙、丁在研究此函数时分别给出命题:甲:函数f(x)的值域为(-1,1);乙:若x1≠x2,则一定有f(x1)≠f(x2);丙:若规定
R),四位同学甲、乙、丙、丁在研究此函数时分别给出命题:甲:函数f(x)的值域为(-1,1);乙:若x1≠x2,则一定有f(x1)≠f(x2);丙:若规定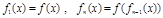 ,
,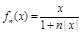 对任意
对任意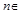 N*恒成立;丁:函数
N*恒成立;丁:函数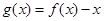 在
在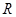 上有三个零点。上述四个命题中你认为正确的是_____________(用甲、乙、丙、丁作答)。
上有三个零点。上述四个命题中你认为正确的是_____________(用甲、乙、丙、丁作答)。 >0,
>0, ≤
≤ 恒成立,则
恒成立,则
 ,则x的取值范围是( )
,则x的取值范围是( ) 


 在区间
在区间 上是减函数,且
上是减函数,且 ,
, ,则
,则 ( )
( )
