题目内容
若f(x)=2sinωx(0<w<1),在区间[0,
]的最大值为
,则ω=( )
| π |
| 3 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先根据题意求得sinwx的最大值,根据区间的最大和最小值和正弦函数的单调性,求得x的值,最后根据sinwx的值求得w.
解答:解:∵f(x)max=(2sinωx)max=
(0<ω<1)
∴在区间[0,
],(sinωx)max=
因为sinωx在区间[0,
]上是单调递增的
所以(sinx)max=sin
=
,这时x=
∵sinωx=
∴ωx=
x=
ω=
故选C
| 2 |
∴在区间[0,
| π |
| 3 |
| ||
| 2 |
因为sinωx在区间[0,
| π |
| 3 |
所以(sinx)max=sin
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
∵sinωx=
| ||
| 2 |
∴ωx=
| π |
| 4 |
| π |
| 3 |
ω=
| 3 |
| 4 |
故选C
点评:本题主要考查了正弦函数的单调性.最为三角函数基础知识,应熟练掌握.

练习册系列答案
相关题目
若f(x)=2sin(ωx+φ)+m,对任意实数t都有f(
+t)=f(
-t),且f(
)=-3,则实数m的值等于( )
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| A、-1 | B、±5 |
| C、-5或-1 | D、5或1 |
 上的最大值是
上的最大值是 ,则ω= .
,则ω= .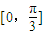 上的最大值是
上的最大值是 ,则ω= .
,则ω= .