题目内容
若f（x）=2sin（ωx+φ）+m，对任意实数t都有f（
+t）=f（
-t），且f（
）=-3，则实数m的值等于（ ）
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| A、-1 | B、±5 |
| C、-5或-1 | D、5或1 |
分析：利用对任意实数t都有f（
+t）=f（
-t）得到x=
为f（x）的对称轴，得到f（
）为最大值或最小值，得到2+m=-3或
-2+m=-3求出m的值．
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
-2+m=-3求出m的值．
解答：解：因为对任意实数t都有f（
+t）=f（
-t），
所以x=
为f（x）的对称轴，
所以f（
）为最大值或最小值，
所以2+m=-3或-2+m=-3
所以m=-5或m=-1
故选C．
| π |
| 8 |
| π |
| 8 |
所以x=
| π |
| 8 |
所以f（
| π |
| 8 |
所以2+m=-3或-2+m=-3
所以m=-5或m=-1
故选C．
点评：解决三角函数的性质问题，一般先化简三角函数，然后利用整体角处理的方法来解决．
练习册系列答案
阅读快车系列答案
相关题目
若f（x）=2sinωx（0＜w＜1），在区间[0，
]的最大值为
，则ω=（ ）
| π |
| 3 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
上的最大值是
，则ω= ．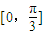
上的最大值是
，则ω= ．