题目内容
16.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点为F1,F2,M为短轴端点,且S△${\;}_{M{F}_{1}{F}_{2}}$=4,离心率为$\frac{\sqrt{2}}{2}$,O为坐标原点.(1)求椭圆C的方程;
(2)过点O作两条射线,与椭圆C分别交于A,B两点,且满足|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|.证明:点O到直线AB的距离为定值.
分析 (1)由椭圆的离心率公式和三角形的面积公式,结合a,b,c的关系,解得a,b,进而得到椭圆方程;
(2)由$|{\overrightarrow{OA}+\overrightarrow{OB}}|=|{\overrightarrow{OA}-\overrightarrow{OB}}|$,两边平方,可得$\overrightarrow{OA}•\overrightarrow{OB}=0$,即两条射线OA、OB互相垂直.讨论直线AB斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理,以及向量垂直的条件:数量积为0,化简整理,可得O到直线的距离为定值.
解答 解:(1)因为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0,b>0)$,
由题意得${S_{△M{F_1}{F_2}}}=\frac{1}{2}×2c×b=4$,$e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,a2=b2+c2,
解得$\left\{\begin{array}{l}{{a}^{2}=8}\\{{b}^{2}=4}\end{array}\right.$,
∴椭圆C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)由$|{\overrightarrow{OA}+\overrightarrow{OB}}|=|{\overrightarrow{OA}-\overrightarrow{OB}}|$,
即有$\overrightarrow{OA}$2+$\overrightarrow{OB}$2+2$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{OA}$2+$\overrightarrow{OB}$2-2$\overrightarrow{OA}$•$\overrightarrow{OB}$,
所以有$\overrightarrow{OA}•\overrightarrow{OB}=0$,即两条射线OA、OB互相垂直.
当直线AB斜率不存在时,容易求出直线AB的方程为$x=\frac{{2\sqrt{6}}}{3}$或x=-$\frac{2\sqrt{6}}{3}$,
此时原点与直线AB的距离$d=\frac{{2\sqrt{6}}}{3}$;
当直线AB斜率存在时,设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+m,
解方程组$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$得x2+2(kx+m)2=8,
即(1+2k2)x2+4kmx+2m2-8=0,
则△=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,
即8k2-m2+4>0,
∴${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}},{x_1}{x_2}=\frac{{2{m^2}-8}}{{1+2{k^2}}}$;
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2
=$\frac{{k}^{2}(2{m}^{2}-8)}{1+2{k}^{2}}$-$\frac{4{k}^{2}{m}^{2}}{1+2{k}^{2}}$+m2=$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$,
由$\overrightarrow{OA}•\overrightarrow{OB}=0$,
∴x1x2+y1y2=0,
∴$\frac{2{m}^{2}-8}{1+2{k}^{2}}$+$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$=0,
即有3m2-8k2-8=0,
∴${m^2}=\frac{{8({k^2}+1)}}{3}$,
∴O到直线AB的距离$d=\frac{|m|}{{\sqrt{{k^2}+1}}}=\frac{{\sqrt{\frac{{8({k^2}+1)}}{3}}}}{{\sqrt{{k^2}+1}}}$=$\frac{{2\sqrt{6}}}{3}$.
综上:O到直线AB的距离为定值$\frac{{2\sqrt{6}}}{3}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的离心率公式和三角形的面积公式,考查向量垂直的条件:数量积为0,同时考查直线和椭圆方程联立,运用韦达定理和点到直线的距离公式,属于中档题.

| A. | 6 | B. | -6 | C. | 8 | D. | -8 |
| A. | cosα≠0是α≠2kπ+$\frac{π}{2}$(k∈Z)的充分必要条件 | |
| B. | 函数f(x)=3ln|x|的零点是(1,0)和(-1,0) | |
| C. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=$\frac{1}{2}$-p | |
| D. | 若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差会改变 |
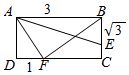 在矩形ABCD中,AB=3,BC=$\sqrt{3}$,$\overrightarrow{BE}=2\overrightarrow{EC}$,点F在边CD上,若$\overrightarrow{AB}•\overrightarrow{AF}=3$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值为( )
在矩形ABCD中,AB=3,BC=$\sqrt{3}$,$\overrightarrow{BE}=2\overrightarrow{EC}$,点F在边CD上,若$\overrightarrow{AB}•\overrightarrow{AF}=3$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值为( )