题目内容
2.实数x取什么值时,复数z=(x2-1)+(x2+3x+2)i是(1)实数(2)在虚轴上(3)实轴的下方(不包括实轴)(4)表示复数z的点在第二象限?分析 (1)直接由z的虚部等于0求得x值;
(2)由实部等于0且虚部不等于0求得x值;
(3)由虚部小于0求解关于x的不等式得答案;
(4)由实部小于0且虚部大于0求解不等式组得答案.
解答 解:(1)当x2+3x+2=0,即x1=-1或x2=-2时,z是实数;
(2)当$\left\{\begin{array}{l}{{x}^{2}-1=0}\\{{x}^{2}+3x+2≠0}\end{array}\right.$,即 x1=1时,z在虚轴上;
(3)当x2+3x+2<0,即x<-2或x>-1时,z在实轴的下方(不包括实轴);
(4)当$\left\{\begin{array}{l}{{x}^{2}+3x+2>0}\\{{x}^{2}-1<0}\end{array}\right.$,即-1<x<1时,点z在第二象限.
点评 本题考查复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
17.如图是高中课程结构图:地理所属课程是( )
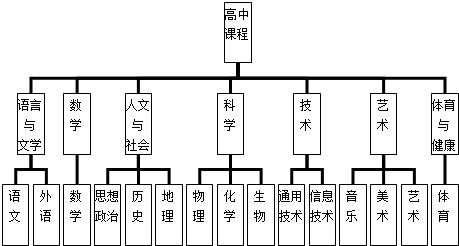

| A. | 人文与社会 | B. | 文科 | C. | 思想政治 | D. | 科学 |
11.命题p:?x1,x2∈R,x1≠x2,有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$>0,命题q:f(x)为R上的增函数;则命题p是命题q的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | C. | 充要 | D. | 不充分且不必要 |
12.下列函数中,既是奇函数,又在区间[0,+∞)上单调递增的函数是( )
| A. | y=tanx | B. | y=sinx | C. | $y={x^{\frac{1}{3}}}$ | D. | $y={x^{\frac{1}{2}}}$ |