题目内容
5．设函数f（x）=（$\frac{1}{2}$）10-ax，其中a为常数，且f（3）=$\frac{1}{16}$．（1）求a的值；
（2）若f（x）≥4，求x的取值范围．
分析 （1）根据f（3）=$\frac{1}{16}$，求出a的值即可；（2）根据指数函数的性质求出x的范围即可．
解答 解：（1）函数f（x）=（$\frac{1}{2}$）10-ax，
由f（3）=$\frac{1}{16}$，得：${（\frac{1}{2}）}^{10-3a}$=$\frac{1}{16}$，
得：3a-10=-4，解得：a=2；
（2）由（1）f（x）=22x-10，
由f（x）≥4，得：22x-10≥22，
故2x-10≥2，解得：x≥6．
点评 本题考查了指数函数的性质，考查求函数的解析式以及解不等式问题，是一道基础题．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
15．已知某批零件的长度误差（单位：毫米）服从正态分布N（0，22），从中随机取一件，其长度误差落在区间（2，4）内的概率为（ ）（若随机变量ξ服从正态分布N（μ，σ2），则P（μ-σ＜ξ＜μ+σ）=68.26%，P（μ-2σ＜ξ＜μ+2σ）=95.44%）
| A． | 4.56% | B． | 13.59% | C． | 27.18% | D． | 31.74% |
16．已知三条不重合的直线m，n，l和两个不重合的平面α，β，下列命题正确的是（ ）
| A． | 若m∥n，n?α，则m∥α | B． | 若l∥n，m⊥n，则l∥m | ||
| C． | 若l⊥α，m⊥β，且l⊥m，则α⊥β | D． | 若α⊥β，α∩β=m，且m⊥n，则n⊥α |
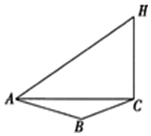某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性，特对其进行了一项测试．如图，这种烟花在燃放点C进行燃放实验，测试人员甲、乙分别在A，B两地（假设三地在同一水平面上），测试人员甲测得A、B两地相距80米且∠BAC=60°，甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒．在A地测得该烟花升至最高点H处的仰角为60°．（已知声音的传播速度为340米∕秒）
20．在△ABC中，点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$，则（ ）
| A． | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B． | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C． | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D． | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |