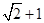题目内容
设双曲线的一个焦点为 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
A. | B. | C. | D. |
D
解析试题分析:不妨设F(-c,0),又B(0.b),所以 ,又双曲线的渐近线方程为
,又双曲线的渐近线方程为 ,所以
,所以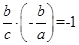 ,即
,即 ,所以
,所以 ,两边同除以
,两边同除以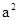 得:
得: ,所以e=
,所以e= .
.
考点:双曲线的简单性质;斜率公式。
点评:求圆锥曲线的离心率是常见题型,常用方法:①直接利用公式 ;②利用变形公式:
;②利用变形公式: (椭圆)和
(椭圆)和 (双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出
(双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出 。
。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若椭圆 的离心率为
的离心率为 ,则双曲线
,则双曲线 的离心率为
的离心率为
A. | B. | C. | D.2 |
抛物线 的准线方程为 ( )
的准线方程为 ( )
A. | B.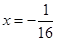 | C. | D. |
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
以 为中心,
为中心, ,
, 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点 ,满足
,满足 ,则该椭圆的离心率为
,则该椭圆的离心率为
A.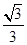 | B. | C. | D. |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B.(1,0) | C.(0,- ) ) | D.(- ,0) ,0) |
若抛物线 上一点
上一点 到
到 轴的距离为3,则点
轴的距离为3,则点 到抛物线的焦点
到抛物线的焦点 的距离为( )
的距离为( )
A. | B. | C. | D. |
 分别为双曲线
分别为双曲线 的左、右焦点,
的左、右焦点, 为双曲线左支上的一点,若
为双曲线左支上的一点,若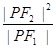 的值为
的值为 ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )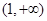




 的焦点F恰好是曲线
的焦点F恰好是曲线 的右焦点,且
的右焦点,且 交点的连线过点F,则曲线
交点的连线过点F,则曲线 的离心率为
的离心率为