题目内容
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
D
解析试题分析:因为 ,所以椭圆
,所以椭圆 的右焦点为
的右焦点为 ,所以
,所以 。
。
考点:椭圆的简单性质;抛物线的简单性质。
点评:注意区分椭圆中 和双曲线中
和双曲线中 关系式的不同。
关系式的不同。

练习册系列答案
相关题目
设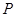 是椭圆
是椭圆 上的点,
上的点,  、
、 是椭圆的两个焦点,则
是椭圆的两个焦点,则 的值为
的值为
| A. 10 | B. 8 | C.6 | D.4 |
双曲线 的焦点坐标是 ( )
的焦点坐标是 ( )
| A.(–2,0),(2,0) | B.(0,–2),(0,2) |
| C.(0,–4),(0,4) | D.(–4,0),(4,0) |
下列方程的曲线关于y轴对称的是( )
| A.x2-x+y2=1 | B.x2y+xy2=1 |
| C.x2-y2=1 | D.x-y="1" |
若抛物线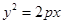 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
如图,椭圆 的四个顶点
的四个顶点 构成的四边形为菱形,若菱形
构成的四边形为菱形,若菱形 的内切圆恰好过焦点,则椭圆的离心率是
的内切圆恰好过焦点,则椭圆的离心率是
A. | B. | C. | D.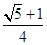 |
直线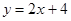 与抛物线
与抛物线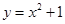 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )
A.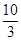 | B.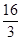 | C.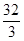 | D.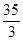 |
 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是



 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为


