题目内容
已知函数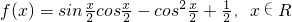
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若已知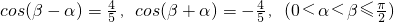 ,求
,求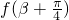 的值.
的值.
解:(I)f(x)= sinx-
sinx- =
= sin(x
sin(x )
)
∴T=2π
(II)∵cos(β-α)=cosαcosβ+sinαsinβ=
cos(β+α)=cosαcosβ-sinαsinβ=-
∴cosαcosβ=0
∵0<α<β≤
∴cosβ=0
∴β=
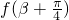 =
= sinβ=
sinβ=
分析:(I)利用二倍角公式将f(x)化简为一个角的一个三角函数的形式,然后直接求出周期;
(II)先根据两角和与差公式展开cos(β-α)和cos(β+α),进而求出cosαcosβ=0,再由角的范围得出β的值,即可求得结果.
点评:本题考查了二倍角公式、两角和与差公式等知识,关键是基本的三角函数的性质的掌握熟练程度,是基础题.
 sinx-
sinx- =
= sin(x
sin(x )
)∴T=2π
(II)∵cos(β-α)=cosαcosβ+sinαsinβ=

cos(β+α)=cosαcosβ-sinαsinβ=-

∴cosαcosβ=0
∵0<α<β≤

∴cosβ=0
∴β=

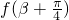 =
= sinβ=
sinβ=
分析:(I)利用二倍角公式将f(x)化简为一个角的一个三角函数的形式,然后直接求出周期;
(II)先根据两角和与差公式展开cos(β-α)和cos(β+α),进而求出cosαcosβ=0,再由角的范围得出β的值,即可求得结果.
点评:本题考查了二倍角公式、两角和与差公式等知识,关键是基本的三角函数的性质的掌握熟练程度,是基础题.

练习册系列答案
相关题目

