题目内容
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.(I)从每班抽取的同学中各抽取一人,求至少有一人及格的概率;
(II)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,求X的分布列和期望.
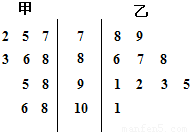
【答案】分析:(I)甲班有4人及格,乙班有5人及格.利用间接法能求出至少有一人及格的概率;
(II)X取值为0,1,2,3,求出相应的概率,可得X的分布列和期望.
解答:解:(Ⅰ)甲班有4人及格,乙班有5人及格.
从每班抽取的同学中各抽取一人有10×10=100种抽法,
则至少有一人及格的概率P=1-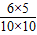 =
=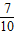 .…(6分)
.…(6分)
(Ⅲ)X取值为0,1,2,3
P(X=0)=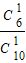 •
•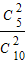 =
=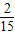 ,
,
P(X=1)=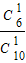 •
•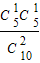 +
+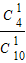 •
•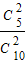 =
=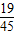 ,
,
P(X=2)=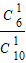 •
•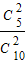 +
+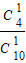 •
•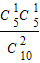 =
=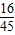 ,
,
P(X=3)=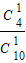 •
•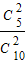 =
=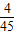 .…(10分)
.…(10分)
所以X的分布列为
所以E(X)=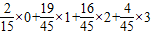 =
= .…(12分)
.…(12分)
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.
(II)X取值为0,1,2,3,求出相应的概率,可得X的分布列和期望.
解答:解:(Ⅰ)甲班有4人及格,乙班有5人及格.
从每班抽取的同学中各抽取一人有10×10=100种抽法,
则至少有一人及格的概率P=1-
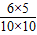 =
=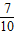 .…(6分)
.…(6分)(Ⅲ)X取值为0,1,2,3
P(X=0)=
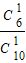 •
•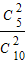 =
=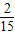 ,
,P(X=1)=
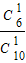 •
•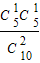 +
+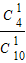 •
•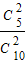 =
=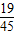 ,
,P(X=2)=
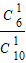 •
•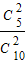 +
+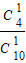 •
•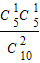 =
=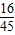 ,
,P(X=3)=
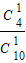 •
•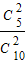 =
=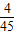 .…(10分)
.…(10分)所以X的分布列为
| X | 1 | 2 | 3 | |
| P(X) | 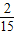 | 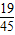 | 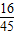 | 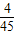 |
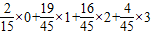 =
= .…(12分)
.…(12分)点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图3所示,成绩不小于90分为及格.
(Ⅰ)甲班10名同学成绩标准差 乙班10名同学成绩标准差(填“>”,“<”);
(Ⅱ)从甲班4名及格同学中抽取两人,从乙班2名80分以下的同学中取一人,求三人平均分不及格的概率.
| 甲 | 乙 | |
| 257 368 24 68 | 7 8 9 10 | 89 678 1235 1 |
(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图5所示,成绩不小于90分为及格.
| 甲 | 乙 | |
| 257 368 58 68 | 7 8 9 10 | 89 678 1235 1 |
(Ⅰ)甲班10名同学成绩的标准差 乙班10名同学成绩的标准差(填“>”,“<”);
(Ⅱ)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(Ⅲ)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,
|
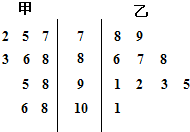 (2012•淄博一模)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(2012•淄博一模)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格. 某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.