题目内容
在极坐标系中，直线θ=
（ρ∈R）与曲线ρ2-8ρcosθ+4=0交于A，B两点，则线段AB的长为（ ）
| π |
| 6 |
A、4
| ||
B、4
| ||
C、2
| ||
D、2
|
考点：简单曲线的极坐标方程
专题：选作题,坐标系和参数方程
分析：先把曲线和直线的极坐标方程化为普通方程，再利用|AB|=2
（d为圆心到直线的距离）即可得出答案．
| r2-d2 |
解答：
解：把极坐标方程化为直角坐标方程可得直线y=
x与圆x2+y2-8x+4=0，圆心为（4，0），半径r为2
，
圆心（4，0）到直线y=
x的距离d=2，
∴|AB|=2
=4
．
故选：A．
| ||
| 3 |
| 3 |
圆心（4，0）到直线y=
| ||
| 3 |
∴|AB|=2
| r2-d2 |
| 2 |
故选：A．
点评：充分理解|AB|=2
（d为圆心到直线的距离）是解题的关键．当然也可以先把交点A、B的坐标求出来，再利用两点间的距离公式即可求出．
| r2-d2 |
练习册系列答案
相关题目
已知集合A={x|x-m＜0}，B={y|y=x2+2x，x∈R}，若A∩B=∅，则实数m的范围为（ ）
| A、m≤-1 | B、m≤0 |
| C、m＜-1 | D、m∈R |
复数
=（ ）
| i2+i3+i4 |
| 1-i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知椭圆
+
=1（a＞b＞0）的右顶点、左焦点分别为A、F，点B（0，-b），若|
+
|=|
-
|，则椭圆的离心率值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| BA |
| BF |
| BA |
| BF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知命题p：?φ∈R，使f（x）=sin（x+φ）为偶函数；命题q：函数y=tanx在（
，π）上单调递减，则下列命题为真命题的是（ ）
| π |
| 2 |
| A、p∧q |
| B、（￢p）∨q |
| C、（￢p）∧（￢q） |
| D、（￢p）∨（￢q） |
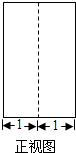三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视图（如图所示）的面积为8，则该三棱柱左视图的面积为（ ）A、2
| ||||
B、
| ||||
C、4
| ||||
D、8
|