题目内容
设a3+b3=2,求证a+b≤2.
思路分析:要证的不等式与所给的条件之间的联系不明显,而且待证式比已知式次数低,直接由条件推出结论的线索不够清晰,于是考虑用反证法.
证明:假设a+b>2,则有a>2-b,从而
a3>8-12b+6b2-b3,
a3+b3>6b2-12b+8=6(b-1)2+2.
所以a3+b3>2,这与题设条件a3+b3=2矛盾,所以,原不等式a+b≤2成立.
误区警示
不能根据已知等式找出几组数值,代入待证不等式中进行验证,验证成立也不能算是证明成功了.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
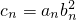 ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn; ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;