题目内容
(文科做)已知等差数列{an}{和正项等比数列{bn},a1=b1=1,a3=b3=2.(1)求an,bn;
(2)设
 ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;(3)设{an}的前n项和为Tn,是否存在常数P、c,使an=p+log2(Tn+c)恒成立?若存在,求P、c的值;若不存在,说明理由.
【答案】分析:(1)由a3=a1+2d,得d= ,由b3=b1q2且q>0得q=
,由b3=b1q2且q>0得q= ,从而可求an,bn;
,从而可求an,bn;
(2)因为cn=(n+1)2n-2,再利用错位相减法可求数列{cn}的前n项和Sn;
(3) ,令n=1,n=3,求得c=
,令n=1,n=3,求得c= ,
, ,再验证下即可.
,再验证下即可.
解答:解:(1)由a3=a1+2d,得d= -------(1分)
-------(1分)
由b3=b1q2且q>0得q= ----(2分)
----(2分)
所以an=a1+(n-1)d= ,bn=b1qn-1=
,bn=b1qn-1= -------(4分)
-------(4分)
(2)因为cn=(n+1)2n-2--------------------------(5分)
故 -----------------①
-----------------①
 ---------------------------②
---------------------------②
所以①-②得: --------------------------(7分)
--------------------------(7分)
所以 --------------------------(9分)
--------------------------(9分)
(3) -------(10分),
-------(10分),
an=p+log2(Tn+c)恒成立,
则当n=1,n=3时,有 -----(12分),
-----(12分),
解得c= ,
, -------(13分)
-------(13分)
p+log2(Tn+c)=log2(2-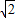 )+
)+ =
= =
= ------(15分)
------(15分)
所以,当c= ,
, 时,an=p+log2(Tn+c)恒成立-------(16分)
时,an=p+log2(Tn+c)恒成立-------(16分)
点评:本题考查等差数列与等比数列的综合,考查数列通项的求解,考查错位相减法求和,解题的关键是确定数列的通项.
 ,由b3=b1q2且q>0得q=
,由b3=b1q2且q>0得q= ,从而可求an,bn;
,从而可求an,bn;(2)因为cn=(n+1)2n-2,再利用错位相减法可求数列{cn}的前n项和Sn;
(3)
 ,令n=1,n=3,求得c=
,令n=1,n=3,求得c= ,
, ,再验证下即可.
,再验证下即可.解答:解:(1)由a3=a1+2d,得d=
 -------(1分)
-------(1分)由b3=b1q2且q>0得q=
 ----(2分)
----(2分)所以an=a1+(n-1)d=
 ,bn=b1qn-1=
,bn=b1qn-1= -------(4分)
-------(4分)(2)因为cn=(n+1)2n-2--------------------------(5分)
故
 -----------------①
-----------------① ---------------------------②
---------------------------②所以①-②得:
 --------------------------(7分)
--------------------------(7分)所以
 --------------------------(9分)
--------------------------(9分)(3)
 -------(10分),
-------(10分),an=p+log2(Tn+c)恒成立,
则当n=1,n=3时,有
 -----(12分),
-----(12分),解得c=
 ,
, -------(13分)
-------(13分)p+log2(Tn+c)=log2(2-
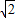 )+
)+ =
= =
= ------(15分)
------(15分)所以,当c=
 ,
, 时,an=p+log2(Tn+c)恒成立-------(16分)
时,an=p+log2(Tn+c)恒成立-------(16分)点评:本题考查等差数列与等比数列的综合,考查数列通项的求解,考查错位相减法求和,解题的关键是确定数列的通项.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
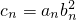 ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;