题目内容
在区间[-1,2]上随机取一个数x,则|x|≤1的概率为 .
【答案】分析:本题利用几何概型求概率.先解绝对值不等式,再利用解得的区间长度与区间[-1,2]的长度求比值即得.
解答:解:利用几何概型,其测度为线段的长度.
∵|x|≤1得-1≤x≤1,
∴|x|≤1的概率为:
P(|x|≤1)=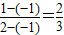 .
.
故答案为: .
.
点评:本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.
解答:解:利用几何概型,其测度为线段的长度.
∵|x|≤1得-1≤x≤1,
∴|x|≤1的概率为:
P(|x|≤1)=
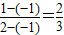 .
.故答案为:
 .
.点评:本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
ax3+ax2-x+10在区间[1,2]上不是单调函数,则a的范围为( )
| 1 |
| 3 |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、(
|