题目内容
如图①所示，在正方形SG1G2G3中，E，F分别是边G1G2、G2G3的中点，D是EF的中点，现沿SE、SF及EF把这个正方形折成一个几何体（如图②使G1G2、G2G3三点重合于一点G），则下列结论中成立的有 （填序号）．①SG⊥面EFG；②SD⊥面EFG；③GF⊥面SEF；④GD⊥面SEF
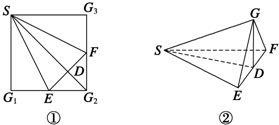
分析：根据题意，在折叠过程中，始终有SG1⊥G1E，SG3⊥G3F，即SG⊥GE，SG⊥GF，由线面垂直的判定定理，易得SG⊥平面EFG．
解答：解：∵在折叠过程中，始终有SG1⊥G1E，SG3⊥G3F，即SG⊥GE，SG⊥GF，∴SG⊥平面EFG，即①正确；
设正方形的棱长为2a，则DG=
a，SD=
a，∵SG2≠DG2+SD2，∴SD与DG不垂直，∴②④不正确；
∵SG⊥GF，∴GF与SF不垂直，∴③不正确；
故答案为：①．
设正方形的棱长为2a，则DG=
| ||
| 2 |
| 3 |
| 2 |
| 2 |
∵SG⊥GF，∴GF与SF不垂直，∴③不正确；
故答案为：①．
点评：本题主要考查了垂直问题的证明，其一般规律是“由已知想性质，由求证想判定”．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
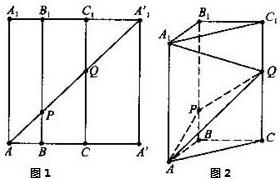如图1所示，在边长为12的正方形AA′A′1A1中，BB1∥CC1∥AA1，且AB=3，BC=4，AA′1分别交BB1，CC1于点P、Q，将该正方形沿BB1、CC1折叠，使得A′A′1与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1，请在图2中解决下列问题：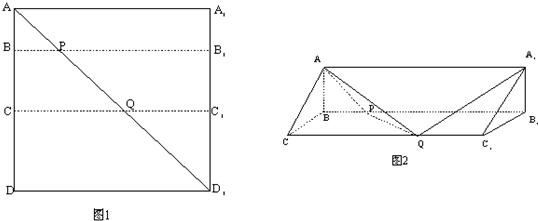
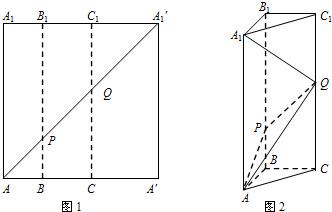如图1所示，在边长为12的正方形AA′A1′A1中，点B，C在线段AA′上，且AB=3，BC=4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P，作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q，将该正方形沿BB1、CC1折叠，使得A′A1′与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1．
中，E、F分别是边
、
的中点，D是EF的中点，现沿SE、SF及EF把这个正方形折成一个几何体（如图乙所示），使
、
、
三点重合于点G，则下面结论成立的是（ ）