题目内容
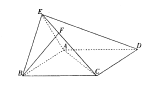
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且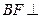 平面ACE。
平面ACE。
(I)求证: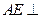 平面BCE;
平面BCE;
(II)求二面角B—AC—E的正弦值;
(III)求点D到平面ACE的距离。
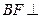 平面ACE。
平面ACE。
(I)求证:
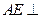 平面BCE;
平面BCE;(II)求二面角B—AC—E的正弦值;
(III)求点D到平面ACE的距离。
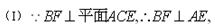
 在直角三角形BCE中,CE=
在直角三角形BCE中,CE=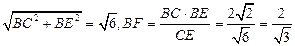
在正方形ABCD中,BG=
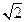 ,在直角三角形BFG中,
,在直角三角形BFG中,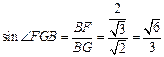 ---9分
---9分(III)
 由(II)可知,在正方形ABCD中,BG=DG,
由(II)可知,在正方形ABCD中,BG=DG,D到平面ACE的距离等于B到平面ACE的距离,BF⊥平面ACE,
线段BF的长度就是点B到平面ACE的距离,即为D到平面ACE的距离.
故D到平面的距离为
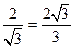 .------------------------------13分
.------------------------------13分另法:用等体积法亦可。
解法二:(Ⅰ)同解法一. ----------------------------------- 4分
(Ⅱ)以线段AB的中点为原点O,OE所在直线为z轴,AB所在直线为x轴,过O点平行于AD的直线为y轴,建立空间直角坐标系O—xyz,如图.
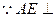 面BCE,BE
面BCE,BE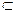 面BCE,
面BCE, 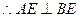 ,
,在
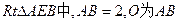 的中点,
的中点,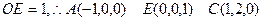
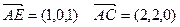
设平面AEC的一个法向量为
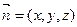 ,
,则
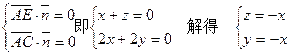
令
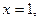 得
得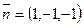 是平面
是平面 AEC的一个法向量.
AEC的一个法向量. 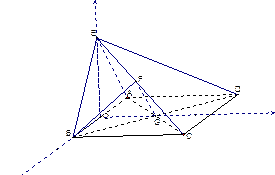
又平面BAC的一个法向量为,
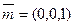
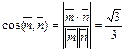
∴二面角B—AC—E的正弦值为
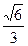 --------------------------------9分
--------------------------------9分
略

练习册系列答案
相关题目
 与正三角形
与正三角形 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形 折成四棱锥
折成四棱锥 ,使
,使 在平面
在平面 上.
上.

 ⊥平面
⊥平面 ;
; 与平面
与平面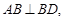 沿BD将
沿BD将 折起,使面
折起,使面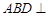 面
面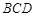 ,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对
,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对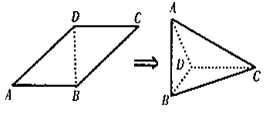
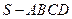 中,底面
中,底面 是
是 正方形,其他四个侧面都是等边三角形,
正方形,其他四个侧面都是等边三角形,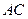 与
与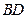 的交点为
的交点为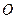 ,
,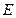 为侧棱
为侧棱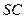 上一点.
上一点. 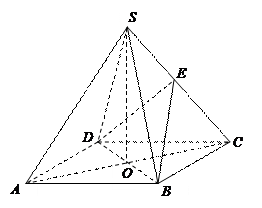
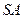 ∥平面
∥平面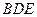 ;
;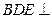 平面
平面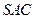 ;
;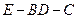 的大小
的大小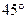 时,试判断点
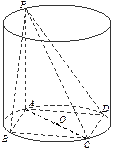
时,试判断点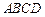 内接于圆柱下底面的圆
内接于圆柱下底面的圆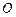 ,
,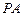 是圆柱的母线,若
是圆柱的母线,若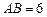 ,
,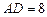 ,此圆柱的体积为
,此圆柱的体积为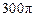 ,求异面直线
,求异面直线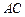 与
与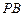 所成角的余弦值.
所成角的余弦值.

 纬
纬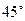 圈上有甲、乙两地,甲地位于东经
圈上有甲、乙两地,甲地位于东经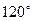 ,乙地位于西经
,乙地位于西经 , 则地球(半径为R)表面上甲、乙两地的最短距离是
, 则地球(半径为R)表面上甲、乙两地的最短距离是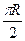 B.
B. 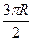 C.
C. 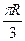 D.
D.