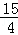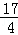题目内容
已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2,若f(x1)=x1<x2,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数为( )
| A.3 | B.4 | C.5 | D.6 |

A
解析

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知函数 ,若
,若 ,
,
且
 ,则
,则 ( )
( )
| A.2 | B.4 | C.8 | D.随 值变化 值变化 |
已知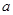 是函数
是函数 的零点,
的零点,
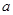 ,则
,则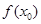 的值满足( )
的值满足( )
A.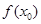 =0 =0 | B.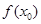 >0 >0 |
C.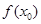 <0 <0 | D.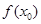 的符号不确定 的符号不确定 |
已知函数f(x)=ax3-3ax+3a-5至少有两个零点,则实数a的取值范围是( )
| A.[1,4] | B.[2,5] | C.[1,5] | D.[-5,-1] |
设函数f(x)=x|x|+bx+c,给出下列四个命题:
①c=0时,y=f(x)是奇函数;
②b=0,c>0时,方程f(x)=0只有一个实数根;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0最多有两个实根.
其中正确的命题是( )
| A.①② | B.②④ | C.①②③ | D.①②④ |
下列函数中,既是偶函数,又在区间(0,+∞) 上单调递减的函数是( )
| A.y=x﹣2 | B.y=x﹣1 | C.y=x2 | D.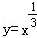 |
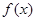 是定义在R上的奇函数,若对于任意给定的不等实数
是定义在R上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式 的解集为( )
的解集为( )



 在
在 内有解,则
内有解,则 的图象可能是( )
的图象可能是( )