题目内容
（2011•湖北）已知定义在R上的奇函数f（x）和偶函数g（x）满足f（x）+g（x）=ax﹣a﹣x+2（a＞0，且a≠0）．若g（a）=a，则f（a）=（ ）
| A．2 | B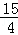． | C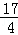． | D．a2 |
B
解析
练习册系列答案
相关题目
若直角坐标平面内的两不同点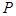
、
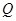满足条件：①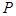、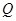都在函数
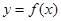的图像上；②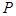、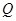关于原点对称，则称点对
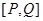是函数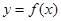的一对“友好点对”（注：点对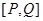与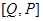
看作同一对“友好点对”）．已知函数
=
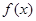，则此函数的“友好点对”有（ ）对．
| A．0 | B．1 | C．2 | D．3 |
设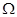
为平面直角坐标系
中的点集，从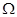中的任意一点
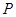作
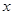轴、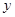
轴的垂线，垂足分别为
，
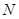，记点的横坐标的最大值与最小值之差为
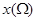，点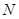的纵坐标的最大值与最小值之差为
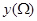.如果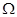是边长为1的正方形，那么
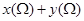的取值范围是（ ）
A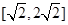． | B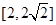． | C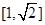． | D． |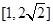
已知对任意实数
，有
为奇函数，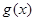
为偶函数，且
时，
，则
时（ ）
| A． | B． |
C． | D． 导数 |
设
，函数
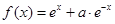的导函数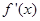
是奇函数，若曲线
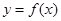的一条切线的斜率是
，则切点的横坐标为（ ）
A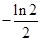． | B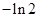． | C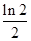． | D． |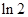
[2013·山东高考]已知函数f(x)为奇函数，且当x＞0时，f(x)＝x2＋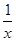
，则f(－1)＝( )
| A．－2 | B．0 | C．1 | D．2 |
(2014·长沙模拟)某公司在甲、乙两地销售一种品牌车,利润(单位：万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位：辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
| A．45.606万元 | B．45.6万元 |
| C．45.56万元 | D．45.51万元 |
定义在R上的偶函数f(x)的部分图象如图所示，则在(－2,0)上，下列函数中与f(x)的单调性不同的是( )
| A．y＝x2＋1 |
| B．y＝|x|＋1 |
C．y＝ |
D．y＝ |
