题目内容
9.在△ABC中,若此三角形有一解,则a,b,锐角A满足的条件为a≥b或a=bsinA.分析 固定角A,画出图形分类讨论得出答案.
解答  解:作∠CAD,使得AC=b,以C为圆心,以a为半径作圆C,则B为圆C与射线AD的交点,如图;
解:作∠CAD,使得AC=b,以C为圆心,以a为半径作圆C,则B为圆C与射线AD的交点,如图;
当a<bsinA时,圆C与射线AD无交点,即△ABC不存在;
当a=bsinA时,圆C与射线AD有一个交点,即这样的三角形只有一个;
当bsinA<a<b时,圆C与射线AD有两个交点,即这样的三角形只有两个;
当a≥b时,圆C与射线AD有一个交点,即这样的三角形只有一个.
综上,若三角形有一解,则a,b,A满足的条件是a≥b或a=bsinA.
故答案为:a≥b或a=bsinA.
点评 本题考查解三角形,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.如果函数f(x)=$\sqrt{x}$在点x=x0处的瞬时变化率是$\frac{\sqrt{3}}{3}$,则x0的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 3 |
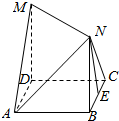 如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点