题目内容
【题目】在①![]() ;②
;②![]() ,这两个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这两个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,设
,设![]() 的面积为
的面积为![]() ,已知 .
,已知 .
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1)见解析(2)![]()
【解析】
(1)如果选择条件①,用余弦定理和三角形面积公式化简即得![]() 的值;如果选择条件②,利用正弦定理化简得
的值;如果选择条件②,利用正弦定理化简得![]() ,再求
,再求![]() 的值;(2)如果选择条件①,先求出
的值;(2)如果选择条件①,先求出![]() ,代入
,代入![]() 即得解;如果选择条件②,求出
即得解;如果选择条件②,求出![]() ,再利用余弦定理即得解.
,再利用余弦定理即得解.
(1)选择条件①:
由題意得![]() .即
.即![]()
整理可得![]() ,
,
又![]() .所以
.所以![]() ,所以
,所以![]() .
.
选择条件②:
因为![]() ,
,
由正弦定理得![]() ,
,
![]() ,
,
即![]()
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
![]() ,所以
,所以![]()
(2)如果选择①,由![]() ,得
,得![]() ,又
,又![]()
则![]() ,解得
,解得![]() .
.
将![]() 代入
代入![]() 中,
中,
得![]() ,
,
解得![]() .
.
如果条件②:![]() ,解得
,解得![]() ,又a=10,
,又a=10,
所以![]() ,所以
,所以![]() .
.

【题目】2019年初,某高级中学教务处为了解该高级中学学生的作文水平,从该高级中学学生某次考试成绩中按文科、理科用分层抽样方法抽取![]() 人的成绩作为样本,得到成绩频率分布直方图如图所示,
人的成绩作为样本,得到成绩频率分布直方图如图所示,![]() ,参考的文科生与理科生人数之比为
,参考的文科生与理科生人数之比为![]() ,成绩(单位:分)分布在
,成绩(单位:分)分布在![]() 的范围内且将成绩(单位:分)分为
的范围内且将成绩(单位:分)分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六个部分,规定成绩分数在
六个部分,规定成绩分数在![]() 分以及
分以及![]() 分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.
分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.

(1)求实数![]() 的值;
的值;
(2)(i)完成下面![]() 列联表;
列联表;
文科生/人 | 理科生/人 | 合计 | |
优秀作文 | 6 | ______ | ______ |
非优秀作文 | ______ | ______ | ______ |
合计 | ______ | ______ | 400 |
(ii)以样本数据研究学生的作文水平,能否在犯错误的概率不超过![]() 的情况下认为获得“优秀作文”与学生的“文理科“有关?
的情况下认为获得“优秀作文”与学生的“文理科“有关?
注: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知100人中同意父母生“二孩”占60%,统计情况如下表:
同意 | 不同意 | 合计 | |
男生 | a | 5 | |
女生 | 40 | d | |
合计 | 100 |
(1)求 a,d 的值,根据以上数据,能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;
(2)将上述调查所得的频率视为概率,现在从所有学生中,采用随机抽样的方法抽取4 位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为 X,求 X 的分布列及数学期望.
附: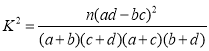
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |