题目内容
8. 如图,在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为A,右焦点为F(c,0).P(x0,y0)为椭圆上一点,且PA⊥PF.
如图,在平面直角坐标系xOy中,椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为A,右焦点为F(c,0).P(x0,y0)为椭圆上一点,且PA⊥PF.(1)若a=3,b=$\sqrt{5}$,求x0的值;
(2)若x0=0,求椭圆的离心率;
(3)求证:以F为圆心,FP为半径的圆与椭圆的右准线x=$\frac{a^2}{c}$相切.
分析 (1)根据a,b,c的关系易得c=2,由PA⊥PF及$\frac{{{x}_{0}}^{2}}{9}+\frac{{{y}_{0}}^{2}}{5}=1$,解得${x}_{0}=\frac{3}{4}$;
(2)联立条件x0=0及PA⊥PF,计算得a2-c2=ac,所以e2+e-1=0,解之即可(注意舍去负值).
(3)联立$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$,以及PA⊥PF得$({x}_{0}+a)[{x}_{0}+\frac{a({b}^{2}-ac)}{{c}^{2}}]=0$,解得${x}_{0}=-\frac{a({a}^{2}-ac-{c}^{2})}{{c}^{2}}$,计算可得PF=$\frac{{a}^{2}}{c}-c$,即得结论.
解答 解:(1)因为a=3,b=$\sqrt{5}$,所以c2=a2-b2=4,即c=2,
由PA⊥PF得,$\frac{{y}_{0}}{{x}_{0}+3}•\frac{{y}_{0}}{{x}_{0}-2}=-1$,即${{y}_{0}}^{2}=-{{x}_{0}}^{2}-{x}_{0}+6$,
又$\frac{{{x}_{0}}^{2}}{9}+\frac{{{y}_{0}}^{2}}{5}=1$,所以$4{{x}_{0}}^{2}+9{x}_{0}-9=0$,
解得${x}_{0}=\frac{3}{4}$或x0=-3(舍去);
(2)当x0=0时,${{y}_{0}}^{2}={b}^{2}$,
由PA⊥PF得,$\frac{{y}_{0}}{a}•\frac{{y}_{0}}{-c}=-1$,
即b2=ac,故a2-c2=ac,
所以e2+e-1=0,解得$e=\frac{\sqrt{5}-1}{2}$(负值已舍);
(3)依题意,椭圆右焦点到直线$x=\frac{{a}^{2}}{c}$的距离为$\frac{{a}^{2}}{c}-c$,且$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$,①
由PA⊥PF得,$\frac{{y}_{0}}{{x}_{0}+a}•\frac{{y}_{o}}{{x}_{0}-c}=-1$,即${{y}_{0}}^{2}=-{{x}_{0}}^{2}+(c-a){x}_{0}+ca$,②
由①②得,$({x}_{0}+a)[{x}_{0}+\frac{a({b}^{2}-ac)}{{c}^{2}}]=0$,
解得${x}_{0}=-\frac{a({a}^{2}-ac-{c}^{2})}{{c}^{2}}$或x0=-a(舍去).
所以PF=$\sqrt{({x}_{0}-c)^{2}+{{y}_{0}}^{2}}$=$\sqrt{({x}_{0}-c)^{2}-{{x}_{0}}^{2}+(c-a){x}_{0}+ca}$=|a-$\frac{c}{a}{x}_{0}$|
=a+$\frac{c}{a}•\frac{a({a}^{2}-ac-{c}^{2})}{{c}^{2}}$=$\frac{{a}^{2}}{c}-c$,
所以以F为圆心,FP为半径的圆与右准线$x=\frac{{a}^{2}}{c}$相切.
点评 本题考查椭圆、圆的方程,考查直线与椭圆的位置关系,考查分析能力与计算能力,属中档题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | (0,$\frac{{\sqrt{2}}}{2}$) | B. | (0,$\frac{{\sqrt{3}}}{3}$) | C. | (0,$\frac{{\sqrt{5}}}{5}$) | D. | ($\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{3}}}{3}$) |
| A. | 1 | B. | -2 | C. | 0 | D. | -1 |
 某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )| A. | 70 | B. | 73 | C. | 75 | D. | 76 |
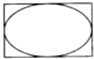 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )| A. | 17.84 | B. | 18.84 | C. | 5.16 | D. | 6.16 |
| A. | {0,1} | B. | {-1,0} | C. | {-1,1} | D. | {-1,0,1} |
 的顶点都在抛物线
的顶点都在抛物线 上,且
上,且 ,则点
,则点 到抛物线的焦点的距离是_____________.
到抛物线的焦点的距离是_____________.