题目内容
下列四个命题: ,
, ”是全称命题;
”是全称命题;
命题“ ,
, ”的否定是“
”的否定是“ ,使
,使 ”;
”;
若 ,则
,则 ;
;
若 为假命题,则
为假命题,则 、
、 均为假命题.
均为假命题.
其中真命题的序号是( )
| A.①② | B.①④ | C.②④ | D.①②③④ |
B
解析试题分析:①因为命题中含有全称量词 ,所以①是全称命题,所以①正确.②全称命题的否定是特称命题,所以命题“
,所以①是全称命题,所以①正确.②全称命题的否定是特称命题,所以命题“ ”的否定是“
”的否定是“ ”,所以②错误.③根据绝对值的意义可知,若
”,所以②错误.③根据绝对值的意义可知,若 ,则
,则 ,所以③错误.④根据复合命题的真假关系可知,若
,所以③错误.④根据复合命题的真假关系可知,若 为假命题,则
为假命题,则 、
、 均为假命题,所以④正确.故真命题是①④.故选B.
均为假命题,所以④正确.故真命题是①④.故选B.
考点:复合命题的真假;命题的真假判断与应用.

练习册系列答案
相关题目
已知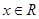 ,则“
,则“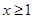 ”是“
”是“ ”的( ).
”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若 ,则
,则 或
或 ”的否定是( )
”的否定是( )
A.若 ,则 ,则 或 或 | B.若 ,则 ,则 且 且 |
C.若 ,则 ,则 或 或 | D.若 ,则 ,则 且 且 |
已知命题p:?x0≥0,使2x0=3,则p的否定是( )
| A.?x<0,使2x≠3 |
| B.?x0<0,使2x0≠3 |
| C.?x0≥0,使2x0≠3 |
| D.?x≥0,使2x≠3 |
在 中,角
中,角 、
、 、
、 所对应的变分别为
所对应的变分别为 、
、 、
、 ,则
,则 是
是 的( )
的( )
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
原命题为“若 互为共轭复数,则
互为共轭复数,则 ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| A.真,假,真 | B.假,假,真 | C.真,真,假 | D.假,假,假 |
下列四个命题:
①利用计算机产生0~1之间的均匀随机数 ,则事件“
,则事件“ ”发生的概率为
”发生的概率为 ;
;
②“ ”是“
”是“ 或
或 ”的充分不必要条件;
”的充分不必要条件;
③命题“在 中,若
中,若 ,则
,则 为等腰三角形”的否命题为真命题;
为等腰三角形”的否命题为真命题;
④如果平面 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面 。
。
其中说法正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
设 、
、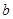 是实数,则“
是实数,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
[2014·徐州检测]用分析法证明:欲使①A>B,只需②C<D,这里①是②的( )
| A.充分条件 | B.必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |