Question

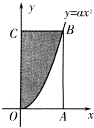（2012•菏泽一模）如图，长方形的四个顶点为O（0，0），A（1，0），B（1，2），C（0，2），曲线y=ax²经过点B、现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是

2

3

．

Answer 1

分析：先求出a，然后根据积分求解出阴影部分的面积，再求解正方形的面积，再将它们代入几何概型计算公式计算出概率．

解答：解：∵曲线y=ax²经过点B（1，2）
∴a=2，y=2x²，
∴长方形部分面积S=1×2=2
阴影部分面积S_阴影=2-∫

1 0

（2x²）dx=2-（

2

3

x3）|

1 0

=2-

2

3

=

4

3

所投的点落在阴影部分的概率P=

4 3

2

=

2

3

故答案为：

2

3

点评：本题考查几何概型的概率，可以为长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．