题目内容
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]()
【解析】试题分析:(1)依题意确定![]() 的定义域,对
的定义域,对![]() 求导,求出函数的单调性,即可求出函数
求导,求出函数的单调性,即可求出函数![]() 的最大值;(2)表示出
的最大值;(2)表示出![]() ,根据其图象上存在一点
,根据其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() 可得
可得![]() ,在
,在![]() 上有解,即可求出实数
上有解,即可求出实数![]() 的取值范围;(3)由
的取值范围;(3)由![]() ,方程
,方程![]() 有唯一实数解,构造函数
有唯一实数解,构造函数![]() ,求出
,求出![]() 的单调性,即可求出正数
的单调性,即可求出正数![]() 的值.
的值.
试题解析:(1)依题意, ![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时, ![]() ,
, ![]()
由![]() ,得
,得![]() ,解得
,解得![]()
由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]()
∵![]() ,∴
,∴![]() 在
在![]() 单调递増,在
单调递増,在![]() 单调递减;所以
单调递减;所以![]() 的极大值为
的极大值为![]() ,此即为最大值
,此即为最大值
(2)![]() ,则有
,则有![]() ,在
,在![]() 上有解,
上有解,
∴![]() ,
, ![]() ,∵
,∵![]() ,所以当
,所以当![]() 时,
时, ![]()
取得最小值![]() ,∴
,∴![]()
(3)由![]() 得
得![]() ,令
,令![]() ,
, 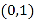
令![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
∴在![]() ,即
,即![]() ,在
,在![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递増,∴
单调递増,∴![]() 极小值
极小值![]() ,令
,令![]() ,即
,即![]() 时方程
时方程![]() 有唯一实数解.
有唯一实数解.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目