[题目]把方程表示的曲线作为函数的图象.则下列结论正确的有( )A.的图象不经过第一象限B.在上单调递增C.的图象上的点到坐标原点的距离的最小值为D.函数不存在零点题目和参考答案——青夏教育精英家教网—

题目内容

【题目】把方程表示的曲线作为函数的图象，则下列结论正确的有（）

A.的图象不经过第一象限

B.在上单调递增

C.的图象上的点到坐标原点的距离的最小值为

D.函数不存在零点

【答案】ACD

【解析】

首先讨论去掉绝对值，并画出函数的图象，直接判断AB，然后数形结合，并结合椭圆和双曲线的性质判断CD选项.

当，方程是不表示任何曲线，故A正确；

当，方程是，即，

如图画出图象

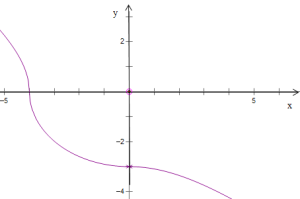
由图判断函数在上单调递减，故B不正确；

由图判断图象上的点到原点距离的最小值点应在的图象上，

即满足，设图象上的点

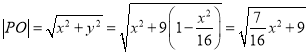
当时取得最小值3，故C正确；

当，即，

函数的零点，就是函数和的交点，

而是曲线，和的渐近线，所以没有交点，由图象可知和，没有交点，

所以函数不存在零点，故D正确.

故选：ACD

练习册系列答案

相关题目

【题目】国家大力提倡科技创新，某工厂为提升甲产品的市场竞争力，对生产技术进行创新改造，使甲产品的生产节能降耗．以下表格提供了节能降耗后甲产品的生产产量(吨)与相应的生产能耗(吨)的几组对照数据．

（吨）
（吨）

（1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

（，）

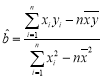（2）已知该厂技术改造前生产吨甲产品的生产能耗为吨，试根据（1）求出的线性回归方程，预测节能降耗后生产吨甲产品的生产能耗比技术改造前降低多少吨？

【题目】正数数列、满足：≥，且对一切k≥2，k，是与的等差中项，是与的等比中项．

（1）若，，求，的值；

（2）求证：是等差数列的充要条件是为常数数列；

（3）记，当n≥2(n)时，指出与的大小关系并说明理由．

【题目】设m，n是两条不同直线，α，β，γ是三个不同平面，给出下列四个命题：

①若m⊥α，n⊥α，则m∥n；②若α∥β，β∥γ，m⊥α，则m⊥γ；

③若m∥α，n∥α，则m∥n；④若m⊥α，m∥β，则α⊥β．

其中正确命题的个数是（）

A.1B.2C.3D.4

【题目】已知椭圆：（）的一个焦点与抛物线：的焦点重合，且离心率为.

（1）求椭圆的标准方程；

（2）过焦点的直线与抛物线交于，两点，与椭圆交于，两点，满足，求直线的方程.

【题目】已知函数.

(1)讨论函数的单调性;

(2)当时，若曲线与曲线存在唯一的公切线，求实数的值;

(3)当时，不等式恒成立，求实数的取值范围.

【题目】已知n为自然数，实数a＞1，解关于x的不等式.

【题目】已知函数（其中为自然对数的底数）．

（1）求的单调性；

（2）若，对于任意，是否存在与有关的正常数，使得成立？如果存在，求出一个符合条件的；否则说明理由．

【题目】数列是公比为正数的等比数列，，；数列前项和为，满足，.

（1）求，及数列，的通项公式；

（2）求.

试题分类