Question

【题目】已知n为自然数，实数a＞1，解关于x的不等式.

Answer 1

【答案】见解析

【解析】

利用对数换底公式，原不等式左端化简，对n是偶数，奇数分类解不等式，即可.

利用对数换底公式，原不等式左端化为：

logax﹣4+12-...+

=[1﹣2+4+...+（﹣2）n﹣1]logax

=logax.

故原不等式可化为logax＞loga（x2﹣a），①

当n为奇数时，＞0，不等式①等价于：logax＞loga（x2﹣a），②

因为a＞1，②式等价于

，

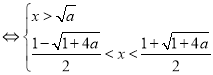因为＜0，＞，

所以，不等式②的解集为{x|＜x＜}.

当n为偶数时，＜0，不等式①等价于logax＜loga（x2﹣a），③

因为a＞1，③式等价于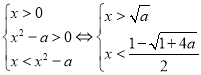或，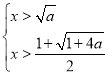

因为，

所以，不等式③的解集为{x|x＞}.

综合得：当n为奇数时，原不等式的解集是{x|}；

当n为偶数时，原不等式的解集是{x|}.