题目内容
证明在抛物线上任取四点所组成的四边形不可能是平行四边形.?
思路分析:不可能是平行四边形,那么到底是什么四边形不太明确,故用反证法.假设是平行四边形,推出矛盾.?
证明:设抛物线方程为y2=2px,A(x1,y1)、?B(x2,y2)?、C(x3,y3)、D(x4,y4)是抛物线上的四点,且四边形ABCD为平行四边形.?
由此可得?
 ?
?
①-②得(y1-y2)(y1+y2)=2p(x1-x2),?
∴kAB=![]() .?
.?
同理,kBC=![]() ,kCD=
,kCD=![]() ,kDA=
,kDA=![]() .?
.?
∵四边形ABCD是平行四边形,?
∴kAB=kCD, kBC=kAD,?
即![]() .?
.?
∴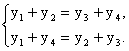 ?
?
∴y1=y3,y2=y4,进而得x1=x3,x2=x4.于是A、C重合,B、D重合.这与A、B、C、D是抛物线上不同的四点的假设矛盾.故四边形ABCD不可能是平行四边形.?
温馨提示:反驳推理中常见的矛盾形式有:(1)与已知公理矛盾,(2)与已知定理矛盾,(3)与已知定义矛盾,(4)与已知条件(或部分条件)矛盾,(5)与由已知条件推出的某正确结论矛盾,(6)与反设自身矛盾,(7)由反设导出两个互相矛盾的结果.

练习册系列答案
相关题目
 已知抛物线y2=2x.
已知抛物线y2=2x.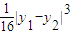 ;
;