题目内容
已知：a＞b＞0，求证：
-
＜
．
| a |
| b |
| a-b |
分析：观察题设，本题中的不等式的证明可以用分析法，逐步寻求不等式成立的条件，由不等式的形式知，可采用平方的办法转化
解答：解：由题意a＞b＞0，故
-
＞0，
＞0
欲证
-
＜
只须证(
-
)2＜(
)2
即a+b-2
＜a-b
只须证b＜
，
只须证b2＜ab
只须证b＜a，显然成立
故a＞b＞0，有
-
＜
| a |
| b |
| a-b |
欲证
| a |
| b |
| a-b |
只须证(
| a? |
| b? |
| a-b? |
即a+b-2
| ab |
只须证b＜
| ab |
只须证b2＜ab
只须证b＜a，显然成立
故a＞b＞0，有
| a |
| b |
| a-b |
点评：本题考查不等式的证明，运用分析法证明不等式是不等式证明的一个常用的方法，尤其适合于题设条件较少的证明
练习册系列答案
相关题目
已知椭圆 (a>b>0)与直线已知椭圆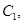
(a>b>0)抛物线
，从每条曲线上取两个点，将其坐标记录于下表中：
|
|
|
4 |
|
1 |
|
|
2 |
4 |
|
2 |
（1）求
的标准方程；
（2）四边形ABCD的顶点在椭圆
上，且对角线AC、BD过原点O，若
,
(i) 求
的最值.
(ii) 求四边形ABCD的面积；
(a＞b＞0)的离心率
, 直线
与椭圆交于P,Q两点, 且OP⊥OQ(如图) ．
；
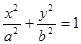(a>b>0)
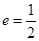，一条准线方程为x＝4 时，求椭圆方程；
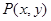是椭圆上一点，在（1）的条件下，求
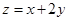的最大值及相应的P点坐标。
(a＞b＞0)，求
的值．