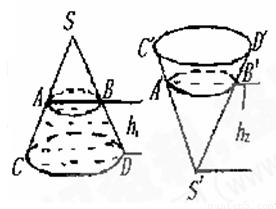
题目内容
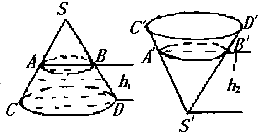 如图,圆锥形封闭容器,高为h,圆锥内水面高为h1,h1=
如图,圆锥形封闭容器,高为h,圆锥内水面高为h1,h1=| h |
| 3 |
| |||
| 3 |
| |||
| 3 |
分析:圆锥正置与倒置时,水的体积不变,另外水面是平行于底面的平面,此平面截得的小圆锥与原圆锥成相似体,它们的体积之比为对应高的立方比.
解答:解:
=(
)3=
,
∴
=
倒置后:V水:V锥=h23:h3=
,
∴h2=(
h3)
=
h.
故答案为:
h.
| VS-AB |
| VS-CD |
| ||
| h |
| 8 |
| 27 |
∴
| V水 |
| V锥 |
| 19 |
| 27 |
| 19 |
| 27 |
∴h2=(
| 19 |
| 27 |
| 1 |
| 3 |
| |||
| 3 |
故答案为:
| |||
| 3 |
点评:此题若用V水=V台计算是比较麻烦的,因为台体的上底面半径还需用h1=
h导出来,我们用V水=V锥-V空,而V空与V锥的体积之间有比例关系,可以直接求出.
| 1 |
| 3 |

练习册系列答案
相关题目
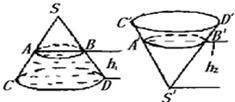 如图,圆锥形封闭容器,高为h,圆锥内水面高为
如图,圆锥形封闭容器,高为h,圆锥内水面高为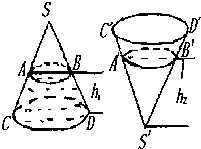 如图,圆锥形封闭容器,高为h,圆锥内水面高为h1,h1=
如图,圆锥形封闭容器,高为h,圆锥内水面高为h1,h1=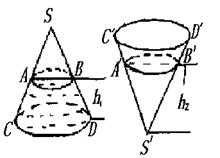
 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为