题目内容
设函数![]() (
(![]() ,b为实数),
,b为实数),![]() .
.
(1)若![]() =0且对任意实数x均有
=0且对任意实数x均有![]() 成立,求
成立,求![]() 表达式;
表达式;
(2)在(1)的条件下,当![]() 时,
时,![]() 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(3)设m>0,n<0且m+n>0, ![]() >0且
>0且![]() 为偶函数,求证:
为偶函数,求证:![]()
(1)∵ ![]() , ∴
, ∴![]() . ……(2分)
. ……(2分)
由![]() 恒成立,知
恒成立,知![]() , ∴ a=1. ……(4分)
, ∴ a=1. ……(4分)
从而![]() .
.
∴ ![]() . ……(5分)
. ……(5分)
(2)由(1)可知![]() , ∴
, ∴![]() . ……(6分)
. ……(6分)
由于![]() 在
在![]() 上是单调函数,知
上是单调函数,知![]() 或
或![]() , ……(8分)
, ……(8分)
解得![]() 或
或![]() . ……(9分)
. ……(9分)
(3)∵ ![]() 是偶函数,∴
是偶函数,∴ ![]() ,得
,得![]() . ……(10分)
. ……(10分)
而a>0,∴![]() 在
在![]() 上为增函数. ……(11分)
上为增函数. ……(11分)
依据![]() ,知:
,知:
当x>0时,-x<0,![]() ;
;
当x<0时,-x>0,![]() .
.
∴ ![]() 是奇函数且
是奇函数且![]() 在
在![]() 上为增函数. ……(13分)
上为增函数. ……(13分)
由m>0,n<0,m+n>0,知![]() ,则
,则![]() ,
,
∴ ![]() ,即
,即![]() . ……(14分)
. ……(14分)

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
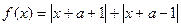 的图象关于y轴对称,函数
的图象关于y轴对称,函数 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线: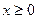 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。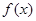 的定义域为实数集,
的定义域为实数集,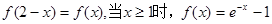 (e为自然对数的底),则必有( )
(e为自然对数的底),则必有( )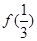 >
>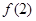 >
> B.
B. 的图象关于y轴对称,函数
的图象关于y轴对称,函数 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线: 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。