题目内容
【题目】已知数列![]() ,
,![]() 为其前
为其前![]() 项的和,满足
项的和,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() ,
,![]() 时
时![]() ;
;
(3)已知当![]() ,且
,且![]() 时有
时有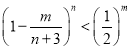 ,其中
,其中![]() ,求满足
,求满足![]() 的所有
的所有![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() 或者
或者![]() .
.
【解析】
(1)利用递推关系,![]() ,
,![]() ,单独求
,单独求![]() ,即可得出;
,即可得出;
(2)法一:直接计算化简即可证明;法二:利用数学归纳法即可证明;
(3)利用“累加求和”方法、不等式的性质、分类讨论即可得出.
(1)解:当![]() 时,
时,
![]()
![]() ,
,
又![]() ,
,![]() .
.
(2)证明:(法一):![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(法二):数学归纳法:
①![]() 时,
时,![]() ,
, ,
,
②假设![]() (
(![]() ,
,![]() )时有
)时有![]() ,
,
当![]() 时,
时,
![]()
![]()
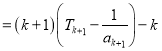
![]()
![]() ,
,
![]() 是原式成立
是原式成立
由①②可知当![]() ,
,![]() 时
时![]() .
.
(3)解: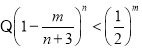 ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
相加得:
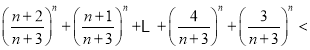
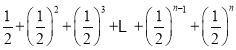 ,
,

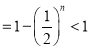 ,
,
即![]() ,两边同时乘以
,两边同时乘以![]() ,
,
![]() ,
,
![]() 时,
时,![]() 无解,
无解,
又当![]() 时;
时;![]() ,
,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() 为偶数,
为偶数,
而![]() 为奇数,不符合
为奇数,不符合
![]() 时,
时,![]() 为奇数,
为奇数,
而![]() 为偶数,不符合.
为偶数,不符合.
综上所述![]() 或者
或者![]() .
.

练习册系列答案
相关题目