题目内容
7.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.证明:OT平分线段PQ(其中O为坐标原点).
分析 (1)由焦距的概念和a,b,c的关系,及正三角形的概念,即可得到a,b方程,解方程可得椭圆的方程;
(2)设T点的坐标为(-3,m),运用直线的斜率公式,由垂直的条件,可得直线PQ的方程,代入椭圆方程,运用韦达定理和中点坐标公式,设PQ的中点为M,结合斜率公式,可得直线OT和OM的斜率相等,即可得证.
解答 解:(1)由已知可得,c=$\sqrt{{a}^{2}-{b}^{2}}$=2,2b=$\sqrt{{a}^{2}+{b}^{2}}$,
解得a2=6,b2=2,
所以椭圆C的标准方程是$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1;
(2)证明:由(1)可得,F的坐标是(-2,0),
设T点的坐标为(-3,m),
则直线TF的斜率kTF=$\frac{m-0}{-3-(-2)}$=-m.
当m≠0时,直线PQ的斜率kPQ=$\frac{1}{m}$.直线PQ的方程是x=my-2.
当m=0时,直线PQ的方程是x=-2,也符合x=my-2的形式.
设P(x1,y1),Q(x2,y2),
将直线PQ的方程与椭圆C的方程联立,
消去x,得(m2+3)y2-4my-2=0,
其判别式△=16m2+8(m2+3)>0.
所以y1+y2=$\frac{4m}{3+{m}^{2}}$,y1y2=$\frac{-2}{3+{m}^{2}}$,
x1+x2=m(y1+y2)-4=$\frac{-12}{3+{m}^{2}}$.
设M为PQ的中点,则M点的坐标为($\frac{-6}{3+{m}^{2}}$,$\frac{2m}{3+{m}^{2}}$),
所以直线OM的斜率kOM=-$\frac{m}{3}$,又直线OT的斜率kOT=-$\frac{m}{3}$,
所以点M在直线OT上,因此OT平分线段PQ.
点评 本题考查椭圆的方程和性质,考查直线方程和椭圆方程联立,运用韦达定理,斜率公式和中点坐标公式,考查运算能力,属于中档题.

| A. | 最大值是f(1),最小值是f(3) | B. | 最大值是f(3),最小值是f(1) | ||
| C. | 最大值是f(1),最小值是f(2) | D. | 最大值是f(2),最小值是f(3) |
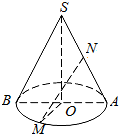 已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.
已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.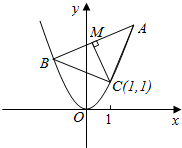 过抛物线y=x2上定点C(1,1)引两条互相垂直的弦CA、CB,作CM⊥AB,M为垂足,求点M的轨迹方程.
过抛物线y=x2上定点C(1,1)引两条互相垂直的弦CA、CB,作CM⊥AB,M为垂足,求点M的轨迹方程.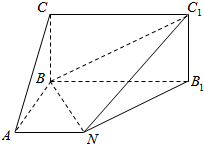 如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.
如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.