题目内容
【题目】已知函数![]() ,
,![]() .
.![]() ,e为自然对数的底数.
,e为自然对数的底数.
(1)如果函数![]() 在(0,
在(0,![]() )上单调递增,求m的取值范围;
)上单调递增,求m的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的一条切线,求实数k的值;
图象的一条切线,求实数k的值;
(3)设![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)1(3)见解析。
(2)1(3)见解析。
【解析】
(1)依题意h′(x)=ex﹣2mx≥0(0,+∞)上恒成立.即![]() 在(0,+∞)上恒成立.即求函数
在(0,+∞)上恒成立.即求函数![]() 的最小值即可;(2)设切点
的最小值即可;(2)设切点![]() ,则切线方程为则
,则切线方程为则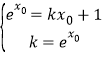 进而得到
进而得到![]() ,令
,令![]() 对函数求导得到函数的单调性和零点即可得到k值(3):要证
对函数求导得到函数的单调性和零点即可得到k值(3):要证![]() ,只要证
,只要证![]() ,两边同时除以
,两边同时除以![]() 令x2﹣x1=t,t>0,即证(t﹣2)et+t+2>0,利用
令x2﹣x1=t,t>0,即证(t﹣2)et+t+2>0,利用![]() =(t﹣2)et+t+2,(t>0)单调性即可证明
=(t﹣2)et+t+2,(t>0)单调性即可证明
:(1)![]() ,
,![]()
要使![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() ,∴
,∴![]() ,令
,令![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
∴当x=1时,![]() 有最小值为
有最小值为![]() ,∴
,∴![]()
(2)∵![]() ,∴
,∴![]() ,设切点为
,设切点为![]() ,则
,则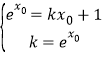
∴![]() ,令
,令![]() ,
,![]()
∴![]() 时,
时,![]() ,
,![]() 单调递减,当k>1时,
单调递减,当k>1时,![]() ,
,![]() 单调递增
单调递增
∴k=1时,![]() ,∴
,∴![]() 时,k=1.∴实数k的值为1.
时,k=1.∴实数k的值为1.
(3)要证![]()
只要证![]() ,两边同时除以
,两边同时除以![]() 得:
得:
![]() ,令
,令![]() 得:
得:![]()
所以只要证:![]() ,令
,令![]()
∴![]() ,
,![]() ,∴
,∴![]()
即![]() ,∴原不等式成立.
,∴原不等式成立.

练习册系列答案
相关题目