Question

【题目】已知函数.

（1）讨论的单调性；

（2）若，且函数只有一个零点，求的最小值.

Answer 1

【答案】（1）答案不唯一，具体见解析（2）的最小值为1

【解析】

（1）首先求出函数的定义域与导函数，讨论的取值范围，分别求出函数的单调区间即可.

（2）解法一：问题等价于只有一个交点，令，可得，记，讨论的取值，确定方程根的个数即可求解；解法二：问题等价于只有一个交点，令，则，令，则，记，作出函数和函数的图像，利用图像的交点即可求解.

解：（1）由题意可知，.

当时，在上单调递增；

当时，在上单调递增，在上单调递减.

（2）解法一：由题意可知，且.

令，

则.

记，（*）

当时，，与相矛盾，此时（*）式无解；

当时，无解；

当时，（*）式的解为，此时有唯一解；

当时，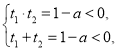

，

所以（*）式只有一个负根，有唯一解，故的最小值为1.

解法二：由题得，

令，则.

再令，则.

记，

函数和函数的图象如图所示：

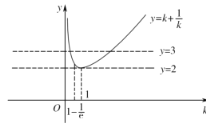
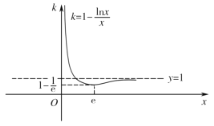
当，即时，显然不成立；

当，即时，由，得方程存在唯一解，且.

此时亦存在唯一解.

综上，的最小值为1.