题目内容
设数列{an}满足关系式a1=2p,an=2p-
证明:∵an=2p-![]() 且a1=2p,
且a1=2p,
得a2=2p-![]() =
=![]() p,a3=2p-
p,a3=2p-![]() =
=![]() p,由此猜想:an=
p,由此猜想:an=![]() p.
p.
(1)当n=1时,a1=![]() p=2p,命题正确.
p=2p,命题正确.
(2)假设当n=k时,命题正确,
即ak=![]() p.
p.
则当n=k+1时,ak+1=2p-![]() =2p-
=2p- p.
p.
∴n=k+1时命题正确.
由(1)(2)可知对任意自然数n∈N*,命题均正确,
而![]() p=p,仅当p=0时成立.
p=p,仅当p=0时成立.
但题设p≠0,∴p不在数列{an}中.

练习册系列答案
相关题目
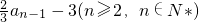
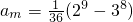 ,试求m
,试求m
 ,试求m
,试求m