题目内容
例2：设数列{an}满足关系式：a1=-1，an=
试证：（1）试求数列{an}的通项公式．
（2）bn=lg（an+9）是等差数列．
（3）若数列{an}的第m项的值
，试求m
【答案】分析：（1）由题意可知
，令Tn=an+9，则Tn是公比为
的等比数列，，由此可知
，从而导出
．
（2）由题意可知bn=lg（an+9）=lg12+（lg2-lg3）n．所以{bn}是公差为（lg2-lg3）的等差数列．
（3）由题设条件得am=（29-38）÷36=
=12×
，即am=a7，所以m=7．
解答：解：（1）∵a1=-1，an=
，
∴
，
∴
，
令Tn=an+9，则Tn是公比为
的等比数列，
，
∴
，
（2）∵bn=lg（an+9）=
，
=lg12+（lg2-lg3）n．
由数列{bn}通项公式可知，{bn}是公差为（lg2-lg3）的等差数列．
（3）若数列数列{an}的第m项的值
，化简得
am=（29-38）÷36=
=12×
由an通项公式可知，am=a7，m=7．
点评：本题考查数列知识人综合运用，解题时要注意计算能力的培养．
，令Tn=an+9，则Tn是公比为的等比数列，，由此可知，从而导出．（2）由题意可知bn=lg（an+9）=lg12+（lg2-lg3）n．所以{bn}是公差为（lg2-lg3）的等差数列．
（3）由题设条件得am=（29-38）÷36=
=12×，即am=a7，所以m=7．解答：解：（1）∵a1=-1，an=
，∴
，∴
，令Tn=an+9，则Tn是公比为
的等比数列，，∴
，（2）∵bn=lg（an+9）=
，=lg12+（lg2-lg3）n．
由数列{bn}通项公式可知，{bn}是公差为（lg2-lg3）的等差数列．
（3）若数列数列{an}的第m项的值
，化简得am=（29-38）÷36=
=12×由an通项公式可知，am=a7，m=7．
点评：本题考查数列知识人综合运用，解题时要注意计算能力的培养．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
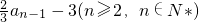
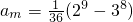，试求m