题目内容
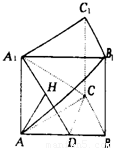
三棱柱中ABC-A1B1C1中,侧棱A1A垂直于底面ABC,B1C1=A1C1,AC1⊥A1B,M,N分别为A1B1,AB中点,求证:
(1)平面AMC1∥平面NB1C;
(2)A1B⊥AM。
(1)平面AMC1∥平面NB1C;
(2)A1B⊥AM。
证明:(1)∵M,N分别为A1B1,AB中点,
∴ ,
,
∴B1N∥AM,
又 ,
,
∴ ,
,
连接MN,在四边形 ,
,
同理得 ,
,
 ,
,
∴平面B1CN∥平面AMC1;
(2)∵B1C1=A1C1,M为A1B1中点,
∴ ,
,
又三棱柱ABC-A1B1C1侧棱A1A垂直于底面ABC,平面A1AB1B垂直于底面ABC交线AB,
∴ ,
,
∴ ,
,
又AC1⊥A1B,
∴ ,
,
 ,
,
∴A1B⊥AM。
∴
 ,
,∴B1N∥AM,
又
 ,
,∴
 ,
,连接MN,在四边形
 ,
,同理得
 ,
, ,
,∴平面B1CN∥平面AMC1;
(2)∵B1C1=A1C1,M为A1B1中点,
∴
 ,
,又三棱柱ABC-A1B1C1侧棱A1A垂直于底面ABC,平面A1AB1B垂直于底面ABC交线AB,
∴
 ,
,∴
 ,
,又AC1⊥A1B,
∴
 ,
, ,
,∴A1B⊥AM。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知直三棱柱A1B1C1-ABC中,D为AB的中点,A1D⊥AB1,且AC=BC,
如图,已知直三棱柱A1B1C1-ABC中,D为AB的中点,A1D⊥AB1,且AC=BC, (2013•济南二模)如图,斜三棱柱A1B1C1-ABC中,侧面AA1C1C⊥底面ABC,底面ABC是边长为2的等边三角形,侧面AA1C1C是菱形,∠A1AC=60°,E、F分别是A1C1、AB的中点.
(2013•济南二模)如图,斜三棱柱A1B1C1-ABC中,侧面AA1C1C⊥底面ABC,底面ABC是边长为2的等边三角形,侧面AA1C1C是菱形,∠A1AC=60°,E、F分别是A1C1、AB的中点.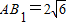 ,
,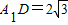 ,求三棱锥A1-ACD的体积;
,求三棱锥A1-ACD的体积;