题目内容
三棱柱中,∠ABC=90°,BB1⊥底面ABC,D为棱AC的中点,且AB=BC=BB1=1。
(1)求二面角A1-BD-C的余弦值;
(2)棱CC1上是否存在一点P,使PD⊥平面A1BD;若存在,试确定P点位置,若不存在,请说明理由。
(1)求二面角A1-BD-C的余弦值;
(2)棱CC1上是否存在一点P,使PD⊥平面A1BD;若存在,试确定P点位置,若不存在,请说明理由。
| 解:(1)以B为坐标原点,射线BC为x轴的正半轴, 建立如图所示的直角坐标系B-xyz, A(0,1,0),C(1,0,0),  , , , , , , , ,设平面  的一个法向量 的一个法向量 , ,又  , ,∴  , ,令x=1,可得  , ,又平面BDC的一个法向量为  , ,设二面角  的大小为 的大小为 ,可知 ,可知 为钝角,故 为钝角,故 。 。(2)设P(1,0,z),则  , ,要使PD⊥平面  ,则需 ,则需 , ,可得  ,故 ,故 , ,即当P是CC1的中点时,所以PD⊥平面  。 。 |
 |

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
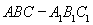
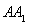
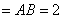
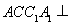
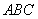
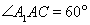
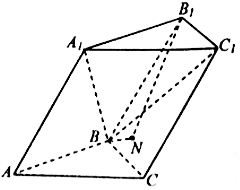

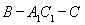

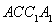

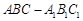 中,△ABC为等边三角形,侧棱
中,△ABC为等边三角形,侧棱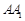 ⊥平面
⊥平面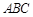 ,
,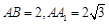 ,D、E分别为
,D、E分别为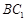 的中点.
的中点.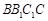 ;
;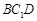 所成角;
所成角;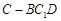 的体积.
的体积.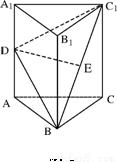
 (2)若直线
(2)若直线 (2)若直线
(2)若直线