题目内容

函数f(x)=Asin(ωx-
π
6
)+1（A＞0，ω＞0）的最大值为3，其图象相邻两条对称轴之间的距离为
π
2
，
（1）求函数f（x）的解析式；
（2）设α∈(0，
π
2
)，则f(
α
2
)=2，求α的值．
（1）∵函数f（x）的最大值为3，∴A+1=3，即A=2，
∵函数图象相邻两条对称轴之间的距离为
π
2
，T=π，所以ω=2．
故函数的解析式为y=2sin（2x-
π
6
）+1．
（2）∵f(
α
2
)=2，所以f(
α
2
)=2sin(α-
π
6
) +1=2，
∴sin(α-
π
6
) =
1
2
，
∵α∈(0，
π
2
)
∴-
π
6
＜α-
π
6
＜ 
π
3
，
∴α-
π
6
=
π
6
，
∴α=
π
3
．
练习册系列答案
相关题目
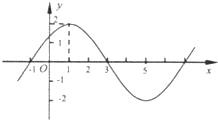精英家教网已知函数f(x)=Asin(ωx+φ)，(A＞0，ω＞0，|φ|＜
π2
，x∈R)的图象的一部分如图所示，则函数f（x）的解析式为
 
．
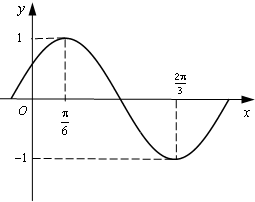精英家教网函数f(x)=Asin(ωx+?) (A＞0，ω＞0，|?|＜
π
2
)部分图象如图所示．
（Ⅰ）求f（x）的最小正周期及解析式；
（Ⅱ）设g（x）=f（x）-cos2x，求函数g（x）在区间x∈[0，
π
2
]上的最大值和最小值．
已知函数f(x)=Asin(ωx+?)，x∈R，(A＞0．ω＞0，0＜?＜
π
2
)的图象与x轴的交点中，相邻两个交点之间的距离为
π
2
，且图象上一个最低点为M(
2π
3
，-2)．
（1）求f（x）的解析式；
（2）设A，B，C是△ABC的三个内角，若cosB=
1
3
，f(
C
2
)=
3
，求sinA．
函数f(x)=Asin(ωx-
π
6
)（A＞0，ω＞0）的最大值为2，其最小正周期为π．
（1）求函数f（x）的解析式；
（2）设α∈(0，
π
2
)，则f(
α
2
)=
2
，求cosα的值．
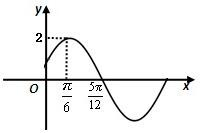（2010•广东模拟）已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）令g(x)=f(x+
π
12
)，判断函数g（x）的奇偶性，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网