题目内容
在△ABC中，a2tanB=b2tanA，则角A与角B的关系为（ ）
| A、A=B |
| B、A+B=90° |
| C、A=B或A+B=90° |
| D、A=B且A+B=90° |
考点：正弦定理,两角和与差的正弦函数
专题：计算题,解三角形
分析：利用正弦定理及同角三角函数关系式把原式化为弦函数，化简后可得sin2A=sin2B，借助正弦函数的性质可得结论．
解答：
解：∵a2tanB=b2tanA，
∴由正弦定理，得sin2AtanB=sin2BtanA，
∴sin2A•
=sin2B•
，即sinAcosA=sinBcosB，
∴sin2A=sin2B，
∴2A=2B或2A+2B=π，即A=B或A+B=
，
故选D．
∴由正弦定理，得sin2AtanB=sin2BtanA，
∴sin2A•
| sinB |
| cosB |
| sinA |
| cosA |
∴sin2A=sin2B，
∴2A=2B或2A+2B=π，即A=B或A+B=
| π |
| 2 |
故选D．
点评：该题考查正弦定理、两角和与差的正弦函数，考查运算求解能力．
练习册系列答案
相关题目
设i是虚数单位，复数
（a∈R）是纯虚数，则实数a的值是（ ）
| a+3i |
| 1-2i |
| A、-6 | B、-2 | C、6 | D、4 |
下列命题中真命题的个数有（ ）个
（1）“奇函数的图象关于原点对称”的逆命题
（2）“若ab=0，则a=0或b=0”的否命题是“若ab≠0，则a≠0且b≠0”
（3）ab≠0是a≠0的充分条件
（4）椭圆的离心率越大，椭圆越扁．
（1）“奇函数的图象关于原点对称”的逆命题
（2）“若ab=0，则a=0或b=0”的否命题是“若ab≠0，则a≠0且b≠0”
（3）ab≠0是a≠0的充分条件
（4）椭圆的离心率越大，椭圆越扁．
| A、1 | B、2 | C、3 | D、4 |
设f（x）在（0，+∞）上是单调递增函数，当n∈N*时，f（n）∈N*，且f[f（n）]=2n+1，则（ ）
| A、f（4）=6 |
| B、f（4）=4 |
| C、f（4）=5 |
| D、f（4）=7 |
直角三角形的斜边长为2，则其内切圆半径的最大值为（ ）
A、
| ||
B、
| ||
C、2
| ||
D、2（
|
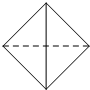
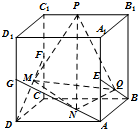已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点，点M、N、Q、P分别在线段DF、AG、BE、C1B1上．以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图不可能是（ ）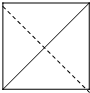
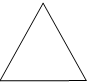
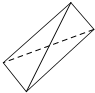
正三棱柱ABC-A1B1C1中，BC=2，AA1=