题目内容
【题目】如下图,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() ,O为
,O为![]() 中点.
中点.
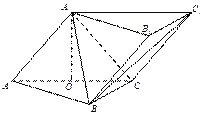
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦;
所成角的正弦;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点![]() 的位置.
的位置.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 为
为![]() 的中点.
的中点.
【解析】(1)因为侧面![]() 底面
底面![]() ,所以只需证明
,所以只需证明![]() 即可.
即可.
(2)可以以O为原点,ON,OC,OA1所在直线为x,y,z轴建立空间直角坐标系,然后用向量的方法求解线面角的问题.
(3)在(2)的基础上也可以用向量来求点E位置.也可以取BC的中点M,连接OM,取BC1的中点E,连接ME,则OM//AB,ME//BB1//AA1,所以平面OMB//平面AA1B,所以OE//平面![]() .从而确定E为BC1的中点.
.从而确定E为BC1的中点.
(Ⅰ)证明:因为![]() ,且O为AC的中点,
,且O为AC的中点,
所以![]()
又由题意可知,平面![]() 平面
平面![]() ,交线为
,交线为![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)如图,以O为原点, ![]() 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.
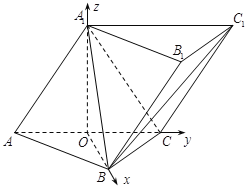
由题意可知, ![]() 又
又![]()
![]()
所以得: ![]()
则有: ![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
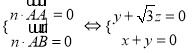 ,令
,令![]() ,得
,得![]()
所以![]()
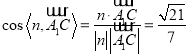
因为直线![]() 与平面
与平面![]() 所成角
所成角![]() 和向量
和向量![]() 与
与![]() 所成锐角互余,所以
所成锐角互余,所以![]()
(Ⅲ)设![]()
即![]() ,得
,得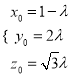
所以![]() 得
得![]()
令![]() 平面
平面![]() ,得
,得![]() ,
,
即![]() 得
得![]()
即存在这样的点E,E为![]() 的中点
的中点

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).