题目内容
若平面向量 =(-1,2)与
=(-1,2)与 的夹角是180°,且|
的夹角是180°,且| |=3
|=3 ,则
,则 坐标为( )
坐标为( )A.(6,-3)
B.(-6,3)
C.(-3,6)
D.(3,-6)
【答案】分析:设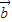 =(x,y),由两个向量的夹角公式得 cos180°=-1=
=(x,y),由两个向量的夹角公式得 cos180°=-1=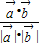 ,利用两个向量的模、数量积公式,化简得x-2y=15,再根据
,利用两个向量的模、数量积公式,化简得x-2y=15,再根据 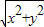 =3
=3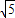 ,解方程组求出x,y的值,进而得到
,解方程组求出x,y的值,进而得到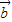 的坐标.
的坐标.
解答:解:设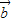 =(x,y),
=(x,y),
由两个向量的夹角公式得 cos180°=-1=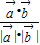 =
=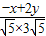 ,
,
∴x-2y=15 ①,∵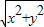 =3
=3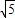 ②,
②,
由①②联立方程组并解得x=3,y=-6,即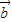 =(3,-6),
=(3,-6),
故选 D.
点评:本题考查两个向量的夹角公式的应用,向量的模的定义,待定系数法求出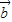 的坐标.
的坐标.
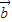 =(x,y),由两个向量的夹角公式得 cos180°=-1=
=(x,y),由两个向量的夹角公式得 cos180°=-1=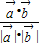 ,利用两个向量的模、数量积公式,化简得x-2y=15,再根据
,利用两个向量的模、数量积公式,化简得x-2y=15,再根据 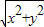 =3
=3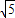 ,解方程组求出x,y的值,进而得到
,解方程组求出x,y的值,进而得到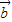 的坐标.
的坐标.解答:解:设
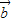 =(x,y),
=(x,y),由两个向量的夹角公式得 cos180°=-1=
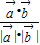 =
=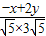 ,
,∴x-2y=15 ①,∵
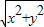 =3
=3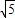 ②,
②,由①②联立方程组并解得x=3,y=-6,即
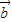 =(3,-6),
=(3,-6),故选 D.
点评:本题考查两个向量的夹角公式的应用,向量的模的定义,待定系数法求出
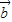 的坐标.
的坐标. 
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
若平面向量
=(-1,2)与
的夹角是180°,且|
|=3
,则
坐标为( )
| a |
| b |
| b |
| 5 |
| b |
| A、(6,-3) |
| B、(-6,3) |
| C、(-3,6) |
| D、(3,-6) |
若平面向量
=(1,x)和
=(2x+3,-x)互相平行,其中x∈R,则|
-
|=( )
| a |
| b |
| a |
| b |
A、2
| ||
B、2或2
| ||
| C、-2或0 | ||
| D、2或10 |