题目内容
14.已知SC是球O的直径,A,B是该球面上的两点,△ABC是边长为$\sqrt{3}$的正三角形,若三棱锥S-ABC的体积为$\sqrt{3}$,则球O的表面积为( )| A. | 16π | B. | 18π | C. | 20π | D. | 24π |
分析 根据题意作出图形,欲求球O的表面积,只须求球的半径r.利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.
解答 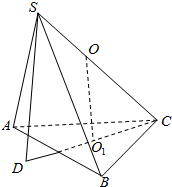 解:根据题意作出图形.
解:根据题意作出图形.
设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
延长CO1交球于点D,则SD⊥平面ABC.
∵CO1=$\frac{2}{3}×\frac{\sqrt{3}}{2}×\sqrt{3}$=1,
∴OO1=$\sqrt{{r}^{2}-1}$,
∴高SD=2OO1=2$\sqrt{{r}^{2}-1}$,
∵△ABC是边长为$\sqrt{3}$的正三角形,
∴S△ABC=$\frac{3\sqrt{3}}{4}$,
∴V三棱锥S-ABC=$\frac{1}{3}$×$\frac{3\sqrt{3}}{4}$×2$\sqrt{{r}^{2}-1}$=$\sqrt{3}$,
∴r=$\sqrt{5}$.则球O的表面积为20π
故选:C.
点评 本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点S到面ABC的距离.

练习册系列答案
相关题目
17.某小型贸易公司为了实现年终10万元利润目标,特制定了一个销售人员年终绩效奖励方案,当销售利润为x万元(4≤x≤10)时,奖金y万元随销售利润x的增加而增加,但奖金总数不超过2万元,同时奖金不超过销售利润的$\frac{1}{2}$,则下列函数中,符合该公司奖励方案的函数模型是(参考数据:lg2≈0.3,lg3≈0.48,lg5≈0.7)( )
| A. | y=0.4x | B. | y=lgx+1 | C. | y=x${\;}^{\frac{3}{2}}$ | D. | y=1.125x |