Question

（2013•许昌二模）已知x₁，x₂是函数f（x）=e^-x-|lnx|的两个零点，则（　　）

• A．

  1

  10

  ＜x₁x₂＜1
• B．

  1

  e

  ＜x₁x₂＜1
• C．1＜x₁x₂＜e
• D．1＜x₁x₂＜10

Answer 1

分析：由题意f（x）=e^-x-|lnx|的零点，即方程e^-x=|lnx|的实数根．因此在同一坐标系内作出函数y=e^-x与y=|lnx|的图象，并设
x₁＜x₂，可得lnx₂＜-lnx₁，推出x₁x₂＜1．再根据x₁＞

1

e

且x₂＞1得到x₁x₂＞

1

e

，由此即可得到本题的答案．

解答：解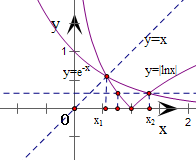：函数f（x）=e^-x-|lnx|的零点，即方程e^-x=|lnx|的实数根
同一坐标系内作出函数y=e^-x与y=|lnx|的图象，如图所示
不妨设x₁＜x₂，可得0＜x₁＜1且x₂＞1
∵0＜-lnx₁＜1，∴lnx₁＞-1，可得x₁＞

1

e

∵x₂＞1，∴x₁x₂＞

1

e

又∵y=e^-x是减函数，可得lnx₂＜-lnx₁，
∴lnx₂+lnx₁＜0，得lnx₁x₂＜0，即x₁x₂＜1
综上所述，可得

1

e

＜x₁x₂＜1
故选：B

点评：本题给出含有指数和对数的基本初等函数，求函数的两个零点满足的条件，着重考查了指数函数、对数函数的图象与性质，以及函数的零点与方程根的关系等知识点，属于中档题．