题目内容
10.某三棱锥的三视图中俯视图是等腰直角三角形,则该三棱锥的外接球的表面积为8π
分析 作出三棱锥的直观图,根据三视图数据计算外接球半径,从而得出面积.
解答 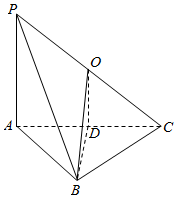 解:根据三视图作出棱锥的直观图如图所示,
解:根据三视图作出棱锥的直观图如图所示,
由三视图可知底面ABC是等腰直角三角形,AB⊥BC,AC=2,PA⊥平面ABC,PA=2.
∴PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=2$\sqrt{2}$,
取AC的中点D,PC的中点O,连结OD,BD,OB,则OD∥PA,OD=$\frac{1}{2}$PA=1,BD=$\frac{1}{2}AC$=1,
∴OD⊥平面ABC,∴OA=OC=OP=$\frac{1}{2}PC$=$\sqrt{2}$,OB=$\sqrt{O{D}^{2}+B{D}^{2}}$=$\sqrt{2}$.
∴OA=OB=OC=OP=$\sqrt{2}$,
即三棱锥的外接球球心为O,半径为$\sqrt{2}$.
∴外接球的面积S=4π×($\sqrt{2}$)2=8π.
故答案为:8π.
点评 本题考查了棱锥的三视图和结构特征,棱锥与外接球的计算,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.“x∈A”是“x∈A∪B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.sin(-1020°)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
5.已知a>0,a≠1,函数$f(x)=\left\{\begin{array}{l}2{x^2},x≥0\\{a^x}-1,x<0\end{array}\right.$在R上是单调函数,若f(a)=5a-2,则实数a=( )
| A. | $\frac{1}{2}或2$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}或5$ |
19.在△ABC中,已知b=2,c=1,B=45°,则a等于( )
| A. | $\frac{\sqrt{14}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{14}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |