题目内容

已知实系数一元二次方程ax2+bx+3=0的一个根为2-i，试确定系数a、b的值.

解：设方程的两个根为x1,x2，其中x1=2-i,

则根据韦达定理得x1+x2=-,x1·x2=.

又因为方程的虚根共轭知  x2=2+i.

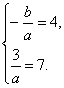于是有  解得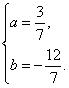

练习册系列答案
相关题目
已知实系数一元二次方程x2+（1+a）x+a+b+1=0的两个实根为x1，x2，且 0＜x1＜1，x2＞1，则
b
a
的取值范围是（　　）
A、(-1，-
1
2
]
B、(-1，-
1
2
)
C、(-2，-
1
2
]
D、(-2，-
1
2
)
已知实系数一元二次方程x2+（1+a）x+a+b+1=0的两个实根为x1、x2，并且0＜x1＜2，x2＞2，则
b
a-1
的取值范围是（　　）

已知实系数一元二次方程，下列结论正确的是（　　　　　）

①是这个方程有实根的充分条件；②是这个方程有实根的必要条件③是这个方程有实根的充要条件④是这个方程有实根的充分条件。

A．③B．①②C．①②③D．①②③④

已知实系数一元二次方程的两个实根为，且 ，则的取值范围是(     )

A．         B．         C．         D．

 

已知实系数一元二次方程的两个实根为，且 ，则的取值范围是(    )

A.     B.      C.     D.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网