Question

已知实系数一元二次方程x²+（1+a）x+a+b+1=0的两个实根为x₁，x₂，且 0＜x₁＜1，x₂＞1，则

b

a

的取值范围是（　　）

• A、(-1，-

  1

  2

  ]
• B、(-1，-

  1

  2

  )
• C、(-2，-

  1

  2

  ]
• D、(-2，-

  1

  2

  )

Answer 1

分析：由方程x²+（1+a）x+1+a+b=0的两根满足0＜x₁＜1＜x₂，结合对应二次函数性质得到

f(0)＞0 f(1)＜0

，然后在平面直角坐标系中，做出满足条件的可行域，分析

b

a

的几何意义，然后数形结合即可得到结论．

解答：解：由程x²+（1+a）x+1+a+b=0的二次项系数为1＞0，
故函数f（x）=x²+（1+a）x+1+a+b图象开口方向朝上
又∵方程x²+（1+a）x+1+a+b=0的两根满足0＜x₁＜1＜x₂，
则

f(0)＞0 f(1)＜0

即

1+a+b＞0 1+1+a+1+a+b＜0

即

1+a+b＞0 3+2a+b＜0

其对应的平面区域如下图阴影示：

∵

b

a

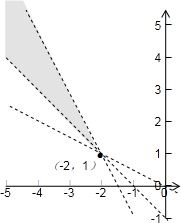
表示阴影区域上一点与原点边线的斜率
由图可知

b

a

∈(-2，-

1

2

)
故选D．

点评：本题考查的知识点是一元二次方程的根的分布与系数的关系，三个二次之间的关系，线性规划，
其中由方程x²+（1+a）x+1+a+b=0的两根满足0＜x₁＜1＜x₂，结合二次函数性质得到

f(0)＞0 f(1)＜0

是解答本题的关键．