题目内容
（2013•许昌二模）设f（x）=|x-3|+|x-4|．
（1）解不等式f（x）≤2；
（2）若存在实数x满足f（x）≤ax-1，试求实数a的取值范围．
（1）解不等式f（x）≤2；
（2）若存在实数x满足f（x）≤ax-1，试求实数a的取值范围．
分析：（1）化简绝对值不等式，通过两个函数的图象求出不等式的解集．
（2）利用（1）的图象直接求出满足f（x）≤ax-1实数a的取值范围即可．
（2）利用（1）的图象直接求出满足f（x）≤ax-1实数a的取值范围即可．
解答：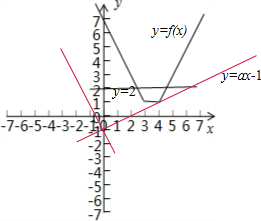
解（1）f(x)=|x-3|+|x-4|=
，
由图象可得f（x）≤2的解集为[
，
]-（5分）
（2）函数y=ax-1，的图象是经过点（0，-1）的直线，
由图象可得a∈(-∞，-2)∪[
，+∞)-----（10分）
解（1）f(x)=|x-3|+|x-4|=
|
由图象可得f（x）≤2的解集为[
| 5 |
| 2 |
| 9 |
| 2 |
（2）函数y=ax-1，的图象是经过点（0，-1）的直线，
由图象可得a∈(-∞，-2)∪[
| 1 |
| 2 |
点评：本题考查绝对值不等式的解法，数形结合的应用，考查分析问题解决问题的能力．
练习册系列答案
名校课堂系列答案
相关题目
（2013•许昌二模）如图，已知PE切圆O于点E，割线PBA交圆O于A，B两点，∠APE的平分线和AE、BE分别交于点C，D