题目内容
((本小题满分12分)已知数列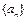 的前
的前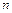 项和为
项和为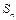 ,
,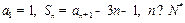 .
.
(Ⅰ)证明:数列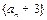 是等比数列;
是等比数列;
(Ⅱ)对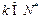 ,设
,设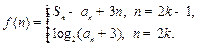 求使不等式
求使不等式
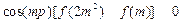 成立的正整数
成立的正整数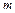 的取值范围.
的取值范围.
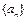 的前
的前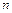 项和为
项和为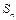 ,
,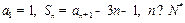 .
.(Ⅰ)证明:数列
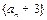 是等比数列;
是等比数列;(Ⅱ)对
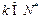 ,设
,设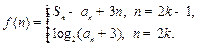 求使不等式
求使不等式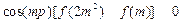 成立的正整数
成立的正整数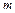 的取值范围.
的取值范围.(1)略
(2)
解:(I)由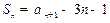 ,则
,则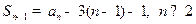 .
.
两式相减得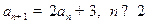 . 即
. 即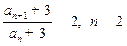 . (2分)
. (2分)
又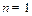 时,
时,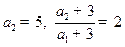 .
.
∴数列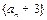 是首项为4,公比为2的等比数列. (4分)
是首项为4,公比为2的等比数列. (4分)
(Ⅱ)由(I)知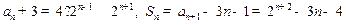 .
.
∴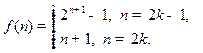 (5分)
(5分)
①当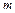 为偶数时,
为偶数时,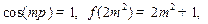
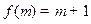 ,
,
∴原不等式可化为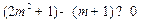 ,
,
即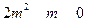 .故不存在合条件的
.故不存在合条件的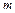 . (7分)
. (7分)
②当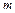 为奇数时,
为奇数时,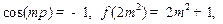
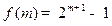 .
.
原不等式可化为 .
.
当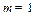 或3时,不等式成立. (9分)
或3时,不等式成立. (9分)
当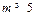 时,
时,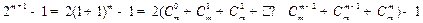
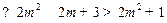 .
.
∴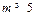 时,原不等式无解. (11分)
时,原不等式无解. (11分)
综合得:当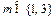 时,不等式
时,不等式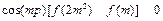 成立. (12分)
成立. (12分)
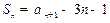 ,则
,则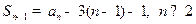 .
.两式相减得
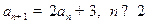 . 即
. 即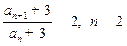 . (2分)
. (2分)又
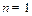 时,
时,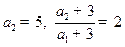 .
.∴数列
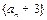 是首项为4,公比为2的等比数列. (4分)
是首项为4,公比为2的等比数列. (4分)(Ⅱ)由(I)知
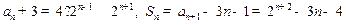 .
.∴
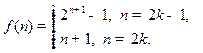 (5分)
(5分)①当
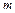 为偶数时,
为偶数时,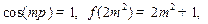
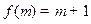 ,
,∴原不等式可化为
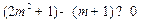 ,
,即
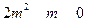 .故不存在合条件的
.故不存在合条件的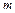 . (7分)
. (7分)②当
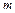 为奇数时,
为奇数时,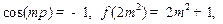
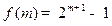 .
.原不等式可化为
 .
.当
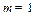 或3时,不等式成立. (9分)
或3时,不等式成立. (9分)当
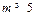 时,
时,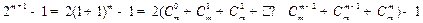
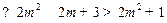 .
. ∴
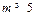 时,原不等式无解. (11分)
时,原不等式无解. (11分)综合得:当
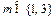 时,不等式
时,不等式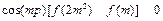 成立. (12分)
成立. (12分)
练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 上的函数
上的函数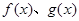 满足
满足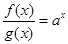 ,
,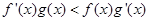 ,
, 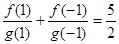 ,有穷数列
,有穷数列 (
(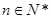 )的前
)的前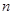 项和等于
项和等于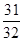 , 则n等于
, 则n等于 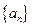 是各项均不为0的等差数列,
是各项均不为0的等差数列,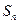 为其前
为其前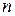 项和,且满足
项和,且满足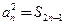 ,令
,令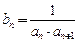 ,数列
,数列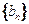 的前n项和为
的前n项和为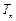 .
.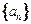 的通项公式及数列
的通项公式及数列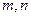
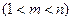 ,使得
,使得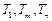 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的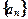 为一等差数列,其中
为一等差数列,其中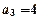 ,
,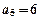 ,
,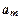
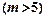 ,使得
,使得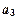 、
、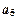 、
、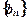 满足
满足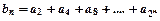 ,求
,求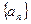 中,
中, ,
, ,令
,令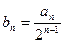 ,
,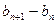 的值 (2)求
的值 (2)求 的前
的前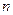 项和.(10分)
项和.(10分)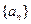 的前
的前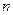 项和为
项和为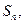
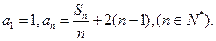
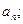

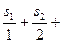
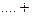
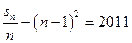 ?若存在,求出
?若存在,求出 的公差为
的公差为 ,且
,且 ,若
,若 ,则
,则 为
为 



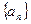 中,
中,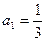 ,且对任意
,且对任意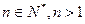 都有
都有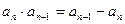 成立,令
成立,令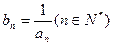 (1)求数列
(1)求数列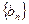 的通项公式;(2)求数列
的通项公式;(2)求数列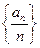 的前n项和
的前n项和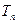 。
。