题目内容
过抛物线x2=4y上两个不同的点A、B分别作抛物线的切线相交于点P,并且满足(1)求点P的轨迹方程;
(2)知点F(0,1),是否存在常数λ使得![]() ?若存在,求出λ的值;若不存在,说明理由.
?若存在,求出λ的值;若不存在,说明理由.
解:(1)设A(x1,![]() ),B(x2,
),B(x2,![]() )(x1≠x2),由x2=4y得y=
)(x1≠x2),由x2=4y得y=![]() ,
,
∴y′=![]() ,∴kPA=
,∴kPA=![]() ,kPB=
,kPB=![]() ,
,
∵![]() ,
,
∴PA⊥PB,
∴kPA·kPB=-1得x1x2=-4,
直线PA的方程是y-![]() =
=![]() (x-x1)即y=
(x-x1)即y=![]() x-
x-![]() .①
.①
直线PB的方程是y-![]() =
=![]() (x-x2)即y=
(x-x2)即y=![]() x-
x-![]() .②
.②
由①②解得x=x1+![]() ,
, (x1,x2∈R).
(x1,x2∈R).
因此,所求点P的轨迹方程是y=-1.
(2)由(1)得![]() =(x1,
=(x1,![]() -1),
-1), ![]() =(x2,
=(x2,![]() -1),
-1),![]() =(
=(![]() ,-2),
,-2),
∵x1x2=-4,
∴![]() -2-
-2-![]() -
-![]() ,
,![]() =
=![]() +
+![]() +2.
+2.
∴![]() +
+![]() =0,即,存在λ=1使得
=0,即,存在λ=1使得![]() +λ
+λ![]() =0成立.
=0成立.

练习册系列答案
相关题目
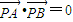 .
.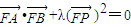 ?若存在,求出λ的值,若不存在,请说明理由.
?若存在,求出λ的值,若不存在,请说明理由.